Definición. Asíntota Horizontal
Sea CL[$ r(x) $] una función racional irreducible.
Si $r$ se aproxima a la recta de ecuación $y=b$ conforme se asignan a $x$ valores cada vez mayores (en valor absoluto ⎯positivos o negativos o en ambas formas⎯), entonces la recta de ecuación $y=b$ se denomina asíntota horizontal de la curva de $r$.
Como ejemplo, consideremos nuevamente la primera función revisada en la Lección 2, a saber, la función no reducible. $r(x)=\frac{1}{x}$.
Sabemos que Dr=-∞, 00, ∞; $D_r=(-\infty,0) \cup (0,\infty)$; contrario a lo que realizamos previamente, analizaremos ahora el comportamiento de las imágenes de rx,$ r(x) $, a medida en que los valores de la variable $ x $ toman valores “sumamente grandes positivos” o valores “sumamente grandes negativos” para ello, al evaluar tenemos:
CL[$ $]
| Considerando valores negativos, cada vez menores. | |
| $x$ | $\frac{1}{x}$ |
| $-10$ | $\frac{1}{-10}=-0.1$ |
| $-100$ | $\frac{1}{-100}=-0.01$ |
| $-1000$ | $\frac{1}{-1000}=-0.001$ |
| $-10000$ | $\frac{1}{-10000}=-0.0001$ |
| $-1000000$ | $\frac{1}{-1000000}=-0.000001$ |
| Considerando valores positivos, cada vez mayores. | |
| $x$ | $\frac{1}{x}$ |
| $10$ | $\frac{1}{10}=0.1$ |
| $100$ | $\frac{1}{100}=0.01$ |
| $1000$ | $\frac{1}{1000}=0.001$ |
| $10000$ | $\frac{1}{10000}=0.0001$ |
| $1000000$ | $\frac{1}{1000000}=0.000001$ |
A partir del registro tabular previo, podemos observar que, tal como corresponde a una relación inversamente proporcional, a medida que $x$ toma valores cada vez más grandes (en valor absoluto), las imágenes correspondientes asumen cada vez valores más pequeños (considerando también el valor absoluto de estas), de acuerdo con lo anterior, el comportamiento gráfico de $ r(x) $ “para valores grandes” es el mostrado a continuación, observa que la relación entre las escalas de los ejes ha sido modificada a fin de poder apreciar adecuadamente la gráfica:
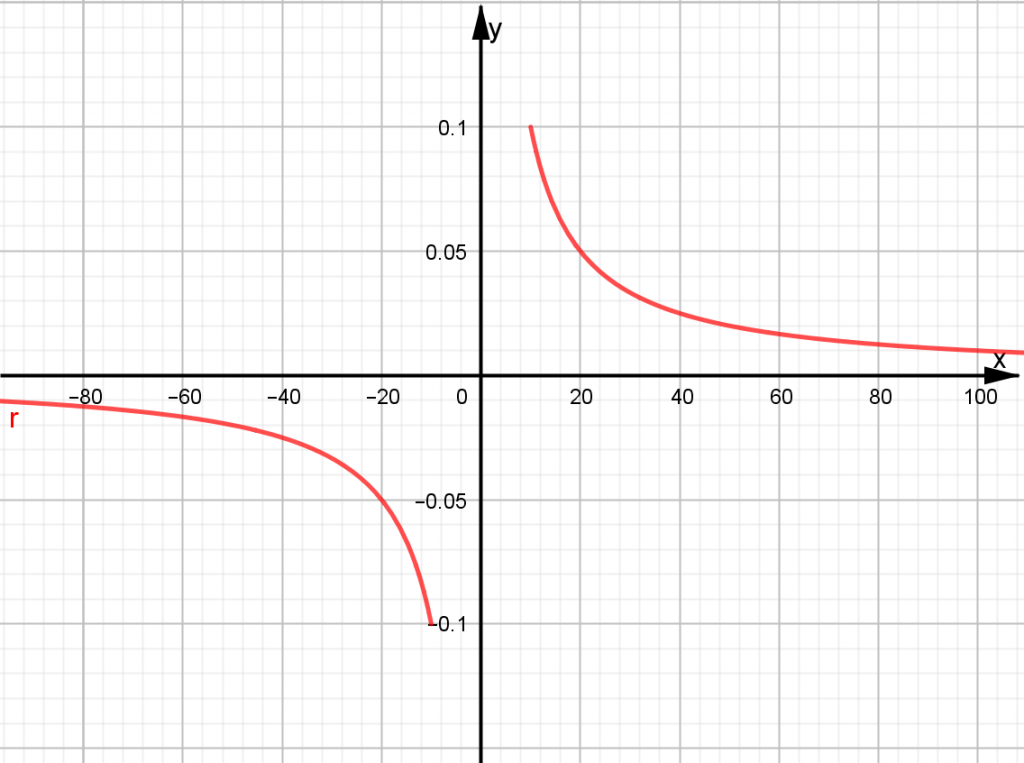
Como se aprecia en la figura anterior, la parte izquierda y la parte derecha de la gráfica de $r(x)$ parece “acercarse” al eje de las abscisas, por lo que, de acuerdo con la definición previa, la recta con ecuación $y=0$ es la asíntota horizontal de $r(x)$.
Consideremos ahora la función con regla de correspondencia $f(x)=\frac{2x^2+1}{x^2-1}$
De nueva cuenta, al analizar el comportamiento de las imágenes de $f(x)$, a medida en que los valores de la variable $x$ toman valores “sumamente grandes positivos” o valores “sumamente grandes negativos” tenemos:
| Considerando valores negativos, cada vez menores. | |
| $x$ | $\frac{2x^2+1}{x^2-1}$ |
| $-10$ | $\frac{2(-10)^2+1}{(-10)^2-1}=\frac{201}{99}\approx 2.0202$ |
| $-100$ | $\frac{2(-100)^2+1}{(-100)^2-1}=\frac{20001}{9999}\approx 2.0003$ |
| $-1000$ | $\frac{2(-1000)^2+1}{(-1000)^2-1}=\frac{2000001}{99999}\approx 2.00021$ |
| $-10000$ | $\frac{2(-10000)^2+1}{(-10000)^2-1}=\frac{200000001}{99999999}\approx 2.00000003$ |
| Considerando valores positivos, cada vez mayores. | |
| $x$ | $\frac{2x^2+1}{x^2-1}$ |
| $10$ | $\frac{2(10)^2+1}{(10)^2-1}=\frac{201}{99}\approx 2.0202$ |
| $100$ | $\frac{2(100)^2+1}{(100)^2-1}=\frac{20001}{9999}\approx 2.0003$ |
| $1000$ | $\frac{2(1000)^2+1}{(1000)^2-1}=\frac{2000001}{99999}\approx 2.0003$ |
| $10000$ | $\frac{2(10000)^2+1}{(10000)^2-1}=\frac{200000001}{99999999}\approx 2.00000003$ |
Al trasladar el registro tabular previo, a su representación gráfica, podemos observar que conforme $x$toma valores cada vez más grandes (en valor absoluto), las imágenes correspondientes asumen valores cada vez más pequeños, los cuales van “acercándose” al valor $y=2$como se aprecia en la siguiente figura, en la cual, nuevamente, la relación entre las escalas de los ejes ha sido modificada a fin de poder visualizar adecuadamente la gráfica:
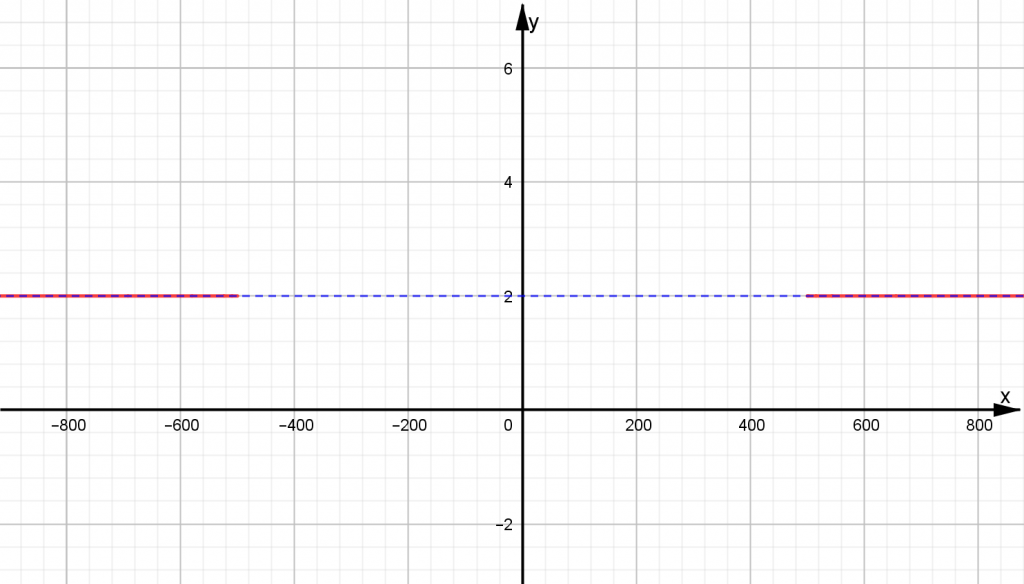
De acuerdo con lo anterior, la gráfica de $r(x)$tiene asíntota horizontal a la recta $y=2$.
Actividad H5P
Consideremos ahora una función polinomial, con el fin de analizar el efecto que, para “valores grandes” de la variable, genera cada una de las potencias en la evaluación de esta. Para ello, realiza la siguiente actividad.