Las funciones trigonométricas y sus derivadas nos permiten resolver varios problemas en diversos contextos. Un ejemplo es el siguiente:
Problema: Un pasillo de ancho r metros da vuelta en ángulo recto. ¿Cuál es la longitud de la varilla más larga que puede girar alrededor de la esquina interior del pasillo, suponiendo que la varilla es delgada y no puede doblarse?
La solución de este problema involucra a las funciones seno, coseno y sus derivadas. Por esta razón nos interesa estudiar la variación de dichas funciones.
Cuando se estudia el comportamiento de una función $f$, la derivada en un punto específico representa la pendiente de la recta tangente a la curva de $f$ en ese punto. El bosquejo de la gráfica de la derivada implica examinar cómo cambian estas pendientes en diferentes puntos donde la función es derivable.
En términos prácticos, para cada punto donde la función original $f$ es derivable, se calcula la pendiente de la recta tangente en ese punto. Estas pendientes se representan en el eje vertical de la gráfica de la derivada. Si la pendiente es positiva, la gráfica de la derivada estará por encima del eje horizontal; si es negativa, estará por debajo. De esta manera, el bosquejo de la gráfica de la derivada proporciona información sobre cómo varían las pendientes y, por ende, la tasa de cambio de la función original en diferentes puntos.
Utilizaremos este razonamiento para obtener la gráfica de la derivada de la función seno en todo su dominio, que son los números reales. Como la función seno es periódica, de periodo $2 \pi$ , bastará con graficar la función derivada en el intervalo $[0,2 \pi]$. Para ir concentrando la información que vayas obteniendo, te sugerimos vaciar la misma en una tabla como la que sigue, tomando en cuenta los intervalos que se te proponen:
Comienza considerando la gráfica de la función seno en el intervalo $[0,\frac{\pi}{2}]$. En este intervalo dibuja las rectas tangentes a la gráfica de la función en algunos puntos claves, por ejemplo, los puntos $0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{2}$ . De estos puntos, el único donde es claro el valor de la pendiente es en $x = \frac{\pi}{2}$ , ¿cuánto vale la pendiente ahí? De los demás puntos no podemos saber a simple vista el valor preciso de las pendientes de sus rectas tangentes, pero ¿podemos decir cuál es su signo? En general, ¿qué se puede decir del signo de las pendientes de las rectas tangentes en los puntos del intervalo $[0, \frac{\pi}{2})$ ? ¿es positivo, negativo, cero, o cambia de signo, según el punto que se tome? Ahora, analiza qué va pasando con el valor de las pendientes conforme la variable x recorres el intervalo de $0$ a $\frac{\pi}{2}$ , ¿van aumentando de valor?, ¿van disminuyendo de valor?, ¿se mantienen constantes? Para lo anterior, auxiliate de los puntos claves.
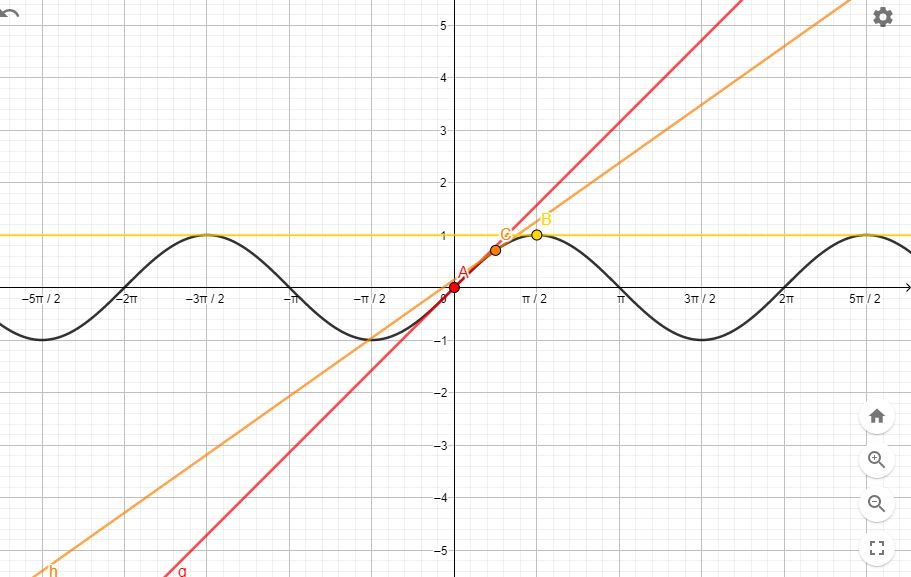
Rectas tangentes a la gráfica de seno
Actividad H5P
Es momento de verificar la información que recabaste con respecto al signo de las pendientes de las rectas tangentes. Acepta el reto: