El área debajo del eje $X$
Ahora vamos a analizar con detalle lo planteado en la situación anterior, lo haremos mediante un ejemplo, vamos a calcula el área bajo la curva de la función $f(x)=-2x+1$ en el intervalo $[1,4]$, esto corresponde a un área que está por debajo del eje $X$.
Vamos a hacer el cálculo tomando los extremos izquierdos de cada subintervalo y a partir de ellos considerar la altura de los rectángulos.
La división del intervalo en subintervalos y considerar los extremos izquierdos para determinar la altura de los rectángulos se ejemplifica en la siguiente imagen
Sumas inferiores debajo del eje $X$
como consideramos subintervalos del mismo tamaño, entonces la longitud de cada subintervalo es:
$\frac{4-1}{n}= \frac{3}{n}$
así podemos determinar los extremos izquierdos de cada subintervalo, quedan como sigue:
$x_1=1$
$x_2=1+\frac{3}{n}$
$x_3=1+2\frac{3}{n}$
$x_4=1+3\frac{3}{n}$
$\vdots$
$x_i=1+(i-1)\frac{3}{n}$
evaluando cada uno de estos extremos izquierdos de los subintervalo en la función, podemos determinar la altura de los respectivos rectángulos, como se muestra en la imagen
Expresiones generales para determinar los rectángulos
El área de cada rectángulo es base por altura, $\frac{3}{n}f(x_i)$. La suma de las áreas de los rectángulos es:
$\displaystyle\sum_{i=1}^{n} \frac{3}{n}f(x_i)=\displaystyle\sum_{i=1}^{n}$
$\frac{3}{n}f(1+[i-1]\frac{3}{n})=\displaystyle\sum_{i=1}^{n}$
$\frac{3}{n}[-2(1+[i-1]\frac{3}{n})+1]$
que cuando $i=1$ nos da el área del primer rectángulo $\frac{3}{n}(-1)=-1$, cuando es $i=2$ nos da el área del segundo rectángulo, y así sucesivamente.
Podemos simplificar la expresión anterior como sigue:
$\displaystyle\sum_{i=1}^{n} \frac{3}{n}[-1-[i-1]\frac{6}{n}]$
ahora, determinamos algunos sumandos y los manipulamos para calcular la sumatoria
$\displaystyle\sum_{i=1}^{n}$
$\frac{3}{n}[-1-[i-1]\frac{6}{n}]=\frac{3}{n}[-1]+\frac{3}{n}[-1-\frac{6}{n}]+\frac{3}{n}[-1-2\frac{6}{n}]+\frac{3}{n}[-1-3\frac{6}{n}]+\dotsc+\frac{3}{n}[-1-(n-1)\frac{6}{n}]$
$=\frac{3}{n}(-1+[-1-\frac{6}{n}]+[-1-2\frac{6}{n}]+[-1-3\frac{6}{n}]+\dotsc+[-1-(n-1)\frac{6}{n}])$
$=\frac{3}{n}(-n-\frac{6}{n}-2\frac{6}{n}-3\frac{6}{n}-\dotsc-(n-1)\frac{6}{n})$
$=\frac{3}{n}(-n-\frac{6}{n}[1+2+3+\dotsc+(n-1)])$
$=\frac{3}{n}(-n-\frac{6}{n}[ \frac{(n-1)n}{2}])$
$=\frac{3}{n}(-n-3[n-1])=\frac{3}{n}(-n-3n+3)=\frac{3}{n}(-4n+3)=-12+ \frac{9}{n}$
ahora tomamos el límite cuando el número de rectángulos tiende a infinito, es decir, cuando $n \rightarrow \infty$
$\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{3}{n}f(x_i)=\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{3}{n}f(1+[i-1]\frac{3}{n})=\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{3}{n}[-1-[i-1]\frac{6}{n}]=\lim\limits_{n \to \infty }[-12+ \frac{9}{n}]=-12$
Por tanto, el área bajo la curva es $-12$.
El resultado dio negativo porque las alturas de todos los rectángulos tienen valor negativo, porque están por debajo del eje $X$. Por tanto, el área bajo la curva puede ser negativa. Esto es diferente al concepto de área de una figura geométrica.
El área bajo la curva será negativa siempre que dicha área esté debajo del eje $X$.
Así, tenemos que $\int_{1}^{4}{-2x+1dx}=-12$, una integral puede ser negativa.
Ahora ya sabemos que una integral puede ser negativa, aunque sea un área. Retomando la situación anterior del área debajo del eje $X$
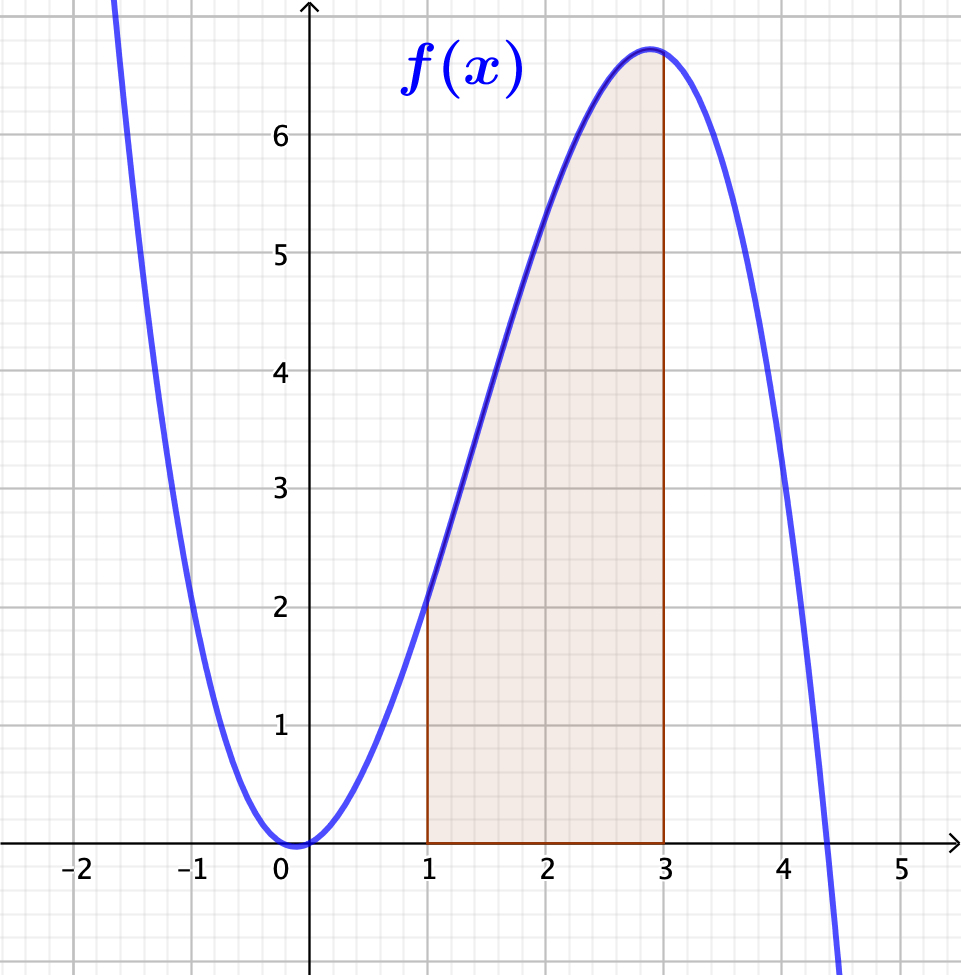
Área bajo la curva en un intervalo de una función $f(x)$
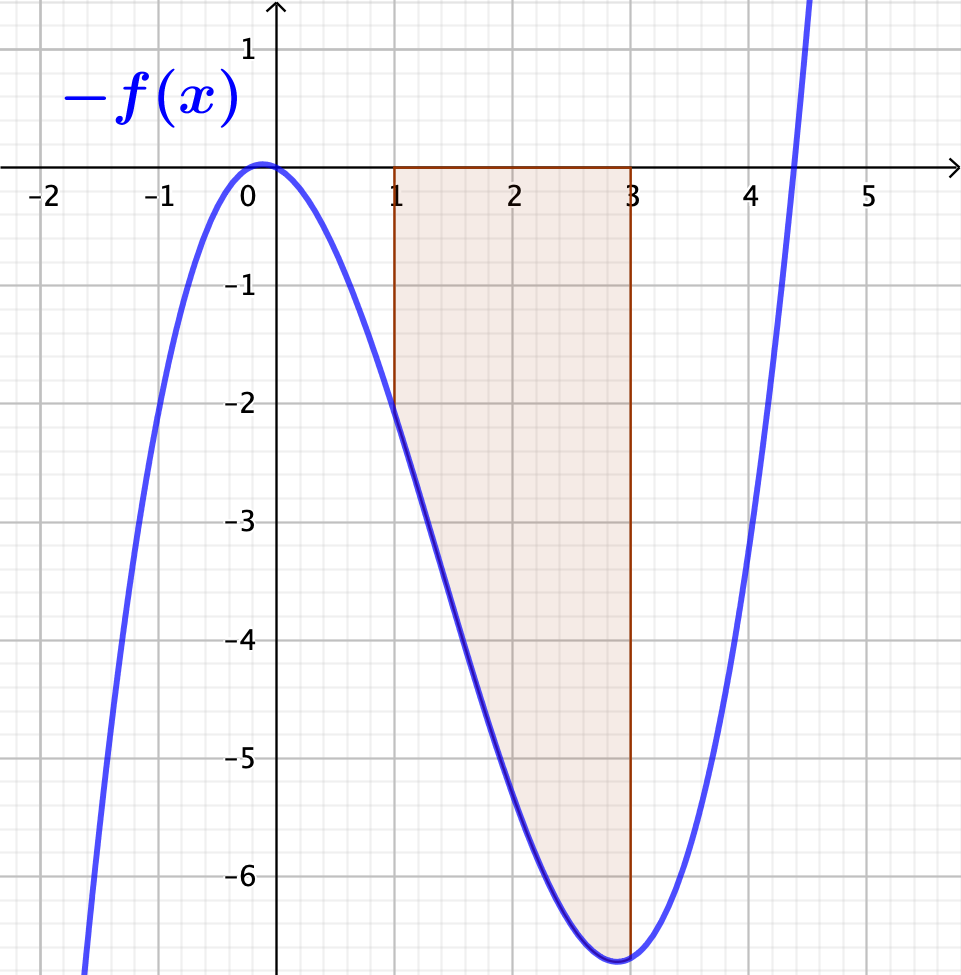
Área bajo la curva en un intervalo de la función $-f(x)$
Si el área bajo la curva de la gráfica de la izquierda es 10, es decir, $\int_{1}^{3}{f(x)dx}=10$, entonces la de la derecha es -10, $\int_{1}^{3}{-f(x)dx}=-10$, pues es la misma solo que está debajo del eje $X$.
Entonces tenemos que
$\int_{1}^{3}{-f(x)dx}=-\int_{1}^{3}{f(x)dx}$
y cómo esto se cumple para cualquier intervalo, podemos expresarlo así
$\int_{a}^{b}{-f(x)dx}=-\int_{a}^{b}{f(x)dx}$
el signo negativo que multiplica a la función “sale” y multiplica a la integral.
El signo negativo es de hecho un $-1$ que está multiplicando
$\int_{a}^{b}{(-1)f(x)dx}=(-1)\int_{a}^{b}{f(x)dx}$
de modo que el $-1$, que es una constante, sale de la integral.
Esto se puede generalizar, no depende del valor de la constante. Es una de las propiedades de la integral:
$\int_{a}^{b}{cf(x)dx}=c\int_{a}^{b}{f(x)dx}$
Intervalo de integración
Vamos a seguir estudiando las propiedades de la integral. Para ello consideramos la siguiente imagen:
Gráfica de dos funciones en un mismo plano
En ella se presentan las gráficas de dos funciones, $g$ y $h$, la primera definida para los reales negativos y la segunda para los reales positivos. Con base en ellas, vamos a calcular $\int_{-2}^{0}{g(x)dx}$ y $\int_{0}^{2}{h(x)dx}$.
Como lo hemos hecho, dividimos el intervalo en subintervalos de igual longitud, y tomamos los extremos izquierdos para determinar la altura de los rectángulos.
Para calcular $\int_{-2}^{0}{g(x)dx}$ la longitud de los subintervalos es:
$\frac{0-(-2)}{n}= \frac{2}{n}$
Entonces, los extremos izquierdos de cada subintervalos son:
$x_1=-2$
$x_2=-2+\frac{2}{n}$
$x_3=-2+2\frac{2}{n}$
$\vdots$
$x_i=-2+(i-1)\frac{2}{n}$
La sumatoria de la suma de las áreas de los rectángulos queda de la siguiente forma:
$\displaystyle\sum_{i=1}^{n} \frac{2}{n}g(x_i)=\displaystyle\sum_{i=1}^{n} \frac{2}{n}g(-2+[i-1]\frac{2}{n})=\displaystyle\sum_{i=1}^{n} \frac{2}{n}(2-[i-1]\frac{2}{n})$
calculamos la sumatoria
$\displaystyle\sum_{i=1}^{n}$
$\frac{2}{n}(2-[i-1]\frac{2}{n})=\frac{2}{n}(2)+\frac{2}{n}(2-\frac{2}{n})+\frac{2}{n}(2-2\frac{2}{n})+\dotsc+\frac{2}{n}(2-(n-1)\frac{2}{n})$
$=\frac{2}{n}[(2)+(2-\frac{2}{n})+(2-2\frac{2}{n})+\dotsc+(2-(n-1)\frac{2}{n})]$
$=\frac{2}{n}[2n-\frac{2}{n}-2\frac{2}{n}-\dotsc-(n-1)\frac{2}{n})]$
$=\frac{2}{n}[2n-\frac{2}{n}(1+2+\dotsc+(n-1))]$
$=\frac{2}{n}[2n-\frac{2}{n}( \frac{(n-1)n}{2})]$
$=\frac{2}{n}[2n-n-1]=\frac{2}{n}[n-1]=2-\frac{2}{n}$
tomando el límite cuando $n \rightarrow \infty$
$\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{2}{n}g(x_i)=\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{2}{n}g(2+[i-1]\frac{2}{n})=\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{2}{n}[-2-[i-1]\frac{2}{n}]=\lim\limits_{n \to \infty }[2+ \frac{2}{n}]=2$
así $\int_{-2}^{0}{g(x)dx}=2$
Hacemos lo mismo para calcular $\int_{0}^{2}{h(x)dx}$
La longitud de los subintervalos es
$\frac{2-0}{n}= \frac{2}{n}$
Entonces, los extremos izquierdos de cada subintervalos son:
$x_1=0$
$x_2=\frac{2}{n}$
$x_3=2\frac{2}{n}$
$\vdots$
$x_i=(i-1)\frac{2}{n}$
La sumatoria de la suma de las áreas de los rectángulos queda de la siguiente forma:
$\displaystyle\sum_{i=1}^{n} \frac{2}{n}h(x_i)=\displaystyle\sum_{i=1}^{n}$
$\frac{2}{n}h([i-1]\frac{2}{n})=\displaystyle\sum_{i=1}^{n}$
$\frac{2}{n}([i-1]\frac{6}{n})=\displaystyle\sum_{i=1}^{n} \frac{12}{n^2}[i-1]$
Calculamos la sumatoria
$\displaystyle\sum_{i=1}^{n}$
$\frac{12}{n^2}[i-1]=0+\frac{12}{n^2}+\frac{12}{n^2}(2)+\dotsc+\frac{12}{n^2}(n-1)$
$=\frac{12}{n^2}[1+2+\dotsc+(n-1)]$
$=\frac{12}{n^2}[ \frac{(n-1)n}{2}]= \frac{6n-6}{n}= 6-\frac{6}{n}$
tomando el límite cuando $n \rightarrow \infty$
$\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{2}{n}h(x_i)=\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{2}{n}h([i-1]\frac{2}{n})=\lim\limits_{n \to \infty }\displaystyle\sum_{i=1}^{n} \frac{12}{n^2}[i-1]=\lim\limits_{n \to \infty }[6-\frac{6}{n}]=6$
así $\int_{0}^{2}{h(x)dx}=6$
En la siguiente gráfica se presentan algunos rectángulos de los cálculos realizados
Gráfica de dos funciones en un mismo plano
Pero ahora, ¿qué pasa si pensamos las gráficas de la imagen como la gráfica de una sola función $f $?
Gráfica de dos funciones en un mismo plano
entonces, si queremos calcular $\int_{-2}^{2}{f(x)dx}$ deberemos calcular el área bajo la curva en el intervalo $[-2,2]$, que será lo mismo que calcular al área bajo la curva en el intervalo $[-2,0]$ y luego sumarla con el área bajo la curva en el intervalo $[0,2]$.
Y como estamos pensado las gráficas como la gráfica de una sola función:
Gráfica de una función $f(x)$
Por tanto, tenemos que
$\int_{-2}^{2}{f(x)dx}=2+6=8$
pero más que el valor, podemos expresar esto de la siguiente forma:
$\int_{-2}^{2}{f(x)dx}=\int_{-2}^{0}{f(x)dx}+\int_{0}^{2}{f(x)dx}$
Lo que nos dice que para calcular el área bajo la curva podemos descomponer el intervalo de integración, calcular las integrales correspondientes en cada intervalo, y luego sumar.
Esto es útil cuando la función es más complicada de integrar como una sola, en esas ocasiones puede ser mejor separarla en pedazos dividiendo el intervalo de integración, e integrar así.
Esta propiedad la podemos expresar así: dados $a<b<c$
$\int_{a}^{c}{f(x)dx}=\int_{a}^{b}{f(x)dx}+\int_{b}^{c}{f(x)dx}$
Actividad H5P
Realiza la siguiente actividad de autoevaluación para verificar tu comprensión de las propiedades de la integral definida.