Te invitamos a que observes el siguiente video; en él conocerás un poco sobre la historia del surgimiento de la Distribución Normal
Elaboró: Miguel A. Rivera Espinosa
Abraham de Moivre, un matemático francés, publicó en 1733 Doctrina de las posibilidades. De Moivre dedujo la distribución normal.
La distribución de probabilidades normal se aplica de manera frecuente para estudiar procesos cuya variable aleatoria es continua.
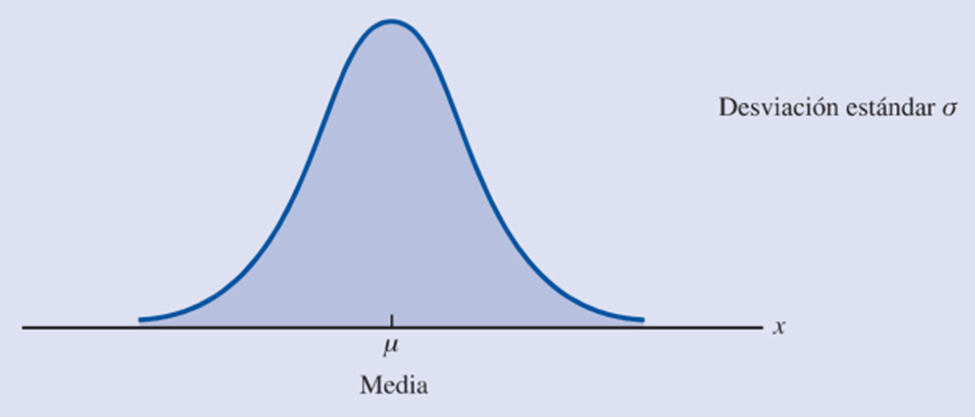
La densidad de probabilidades de esta distribución se caracteriza por los parámetros $\bar{x}$ y $\sigma$, es decir, su media y su desviación estándar, respectivamente; esta distribución es simétrica respecto a el valor de su media, y tiene una forma de campana. La distribución normal es importante porque es un modelo apropiado para explicar la distribución de muchas medidas, tales como estatura, peso, las puntuaciones en un examen, resultados de mediciones científicas, precipitación pluvial y las pruebas de aptitud, por mencionar algunos casos. La manera de tipificar cualquier curva de tipo normal es dibujando una curva en forma de campana indicando en el centro de la misma el valor de su media ($\bar{x}$) y a un lado en la parte superior de preferencia el valor de la desviación estándar ($\sigma$). ver figura 2.
Elaboró: Miguel A. Rivera Espinosa
En los libros de estadística se puede simbolizar a la media por $\bar{x}$ o por la letra griega mu $\mu $.
La función que tipifica matemáticamente este comportamiento de la también llamada campana de Gauss es:
Función de densidad de probabilidad normal, está dada por la siguiente ecuación:
$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{{e}^{\frac{-{{(x-\sigma )}^{2}}}{2{{\sigma }^{2}}}}}$.
Donde:
$ \mu \equiv media\equiv \bar{x} $
$\sigma \equiv desviaci\acute{o}n\_es\operatorname{t}\grave{a}ndar $
$e\equiv 2.71828 $
Observaciones importantes acerca de las características de las distribuciones normales
Las siguientes son observaciones importantes acerca de las características de las distribuciones normales.
1.- Toda la familia de distribuciones normales se diferencia por medio de dos parámetros: la media y la desviación estándar.
2.- El punto más alto de una curva normal se encuentra sobre la media, la cual coincide con la mediana y la moda.
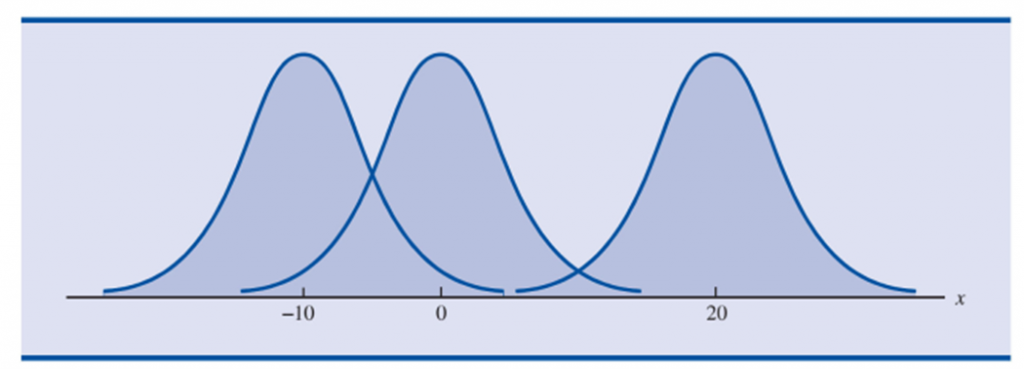
3.- La media de una distribución normal puede tener cualquier valor: negativo, positivo o cero.
Elaboró: Miguel A. Rivera Espinosa
4. La distribución normal es simétrica, siendo la forma de la curva normal al lado izquierdo de la media, la imagen especular (el reflejo) de la forma al lado derecho de la media.
5.- Las colas de la curva normal se extienden al infinito en ambas direcciones y en teoría jamás tocan el eje horizontal, es decir, su comportamiento es asintótico.
6.- Dado que es simétrica, la distribución normal no es sesgada, su sesgo es cero.
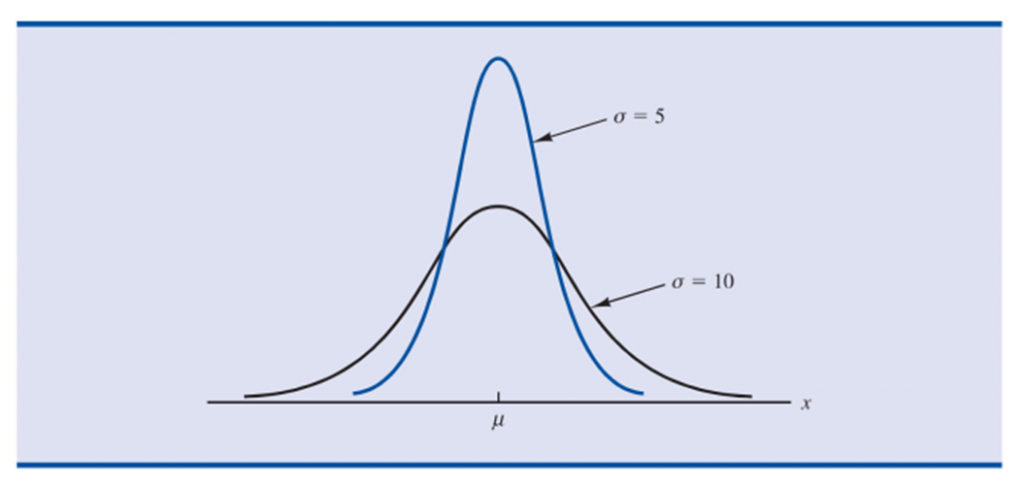
7.- La desviación estándar determina qué tan plana y ancha es la curva normal. Desviaciones estándar grandes corresponden a curvas más planas y más anchas, lo cual indica mayor variabilidad en los datos. Esto se muestra en la figura 4.
Elaboró: Miguel A. Rivera Espinosa
8. Las probabilidades correspondientes a la variable aleatoria normal, se dan mediante áreas bajo la curva normal. Toda el área bajo la curva de una distribución normal es 1. Como esta distribución es simétrica, el área bajo la curva y a la izquierda de la media es 0.50 y el área bajo la curva y a la derecha de la media es 0.50.
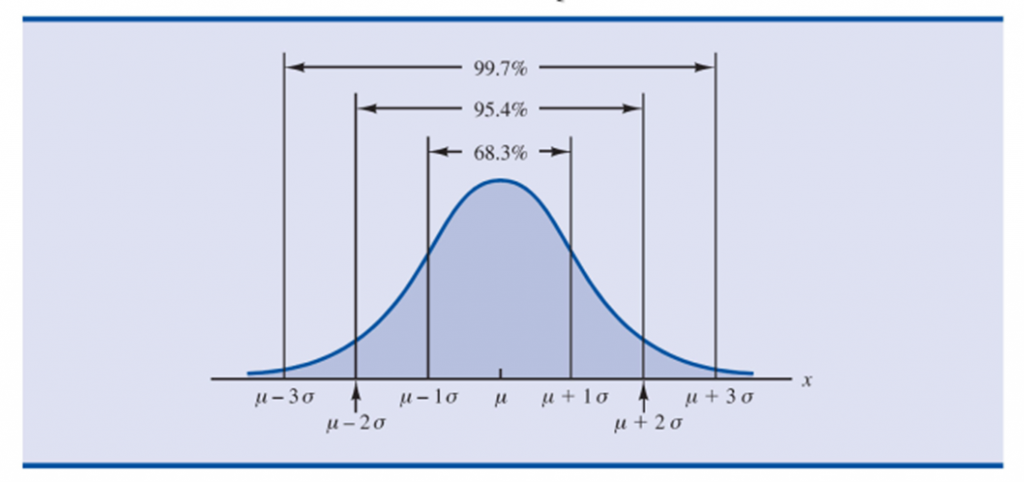
9. Los porcentajes de los valores que se encuentran en algunos intervalos comúnmente usados son:
a. 68.3% de los valores de una variable aleatoria normal se encuentran más o menos una desviación estándar de la media.
b. 95.4% de los valores de una variable aleatoria normal se encuentran más o menos dos desviaciones estándar de la media.
c. 99.7% de los valores de una variable aleatoria normal se encuentran más o menos tres desviaciones estándar de la media.
En la figura 5 aparece una gráfica de las propiedades a, b y c, la explicación anterior es la base para fundamentar la regla empírica.
Elaboró: Miguel A. rivera Espinosa
Área bajo la curva Normal y manejo de tablas
Las áreas bajo la curva para cualquier distribución normal se pueden encontrar, utilizando una tabla normal estándar y cambiando a unidades estándares la escala de unidades reales.

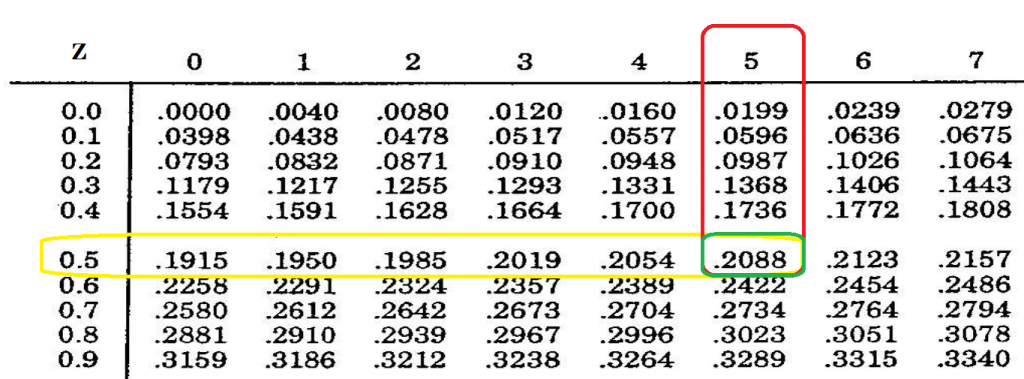
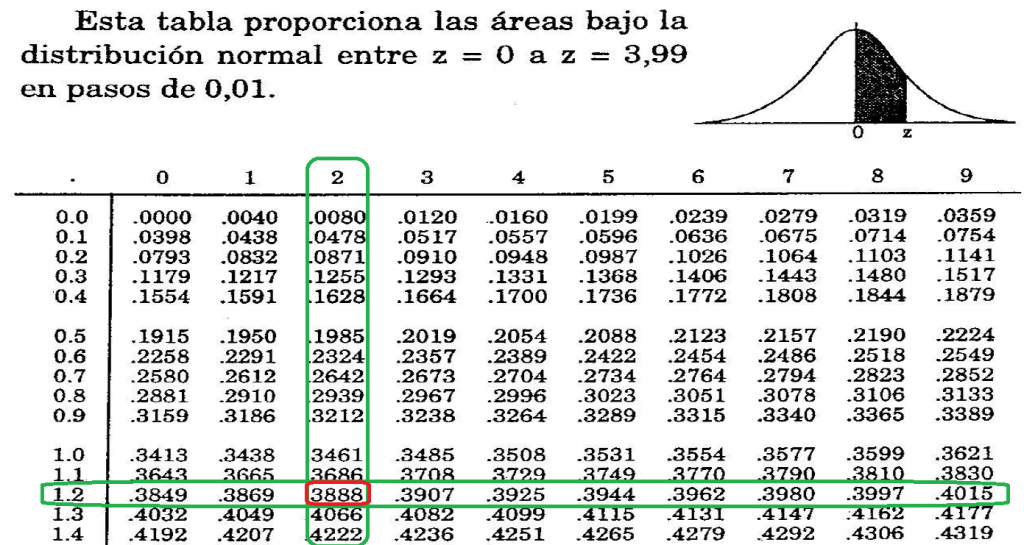
La tabla muestra el área bajo la curva (es decir, la probabilidad de que un valor quede en ese intervalo) entre la media y valores seleccionados de z.
Si buscamos un valor de Z = 0.55, el área bajo la curva se puede leer en la intersección de la fila Z = 0.5 y la columna .05
Elaboró: Anakaren Vega Rodríguez
La parte sombreada de la figura corresponde al área bajo la curva que se puede leer directamente en la tabla.
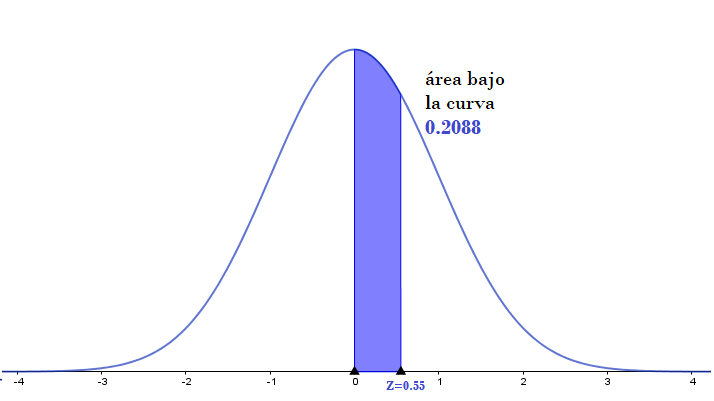
Elaboró: Anakaren Vega Rodríguez
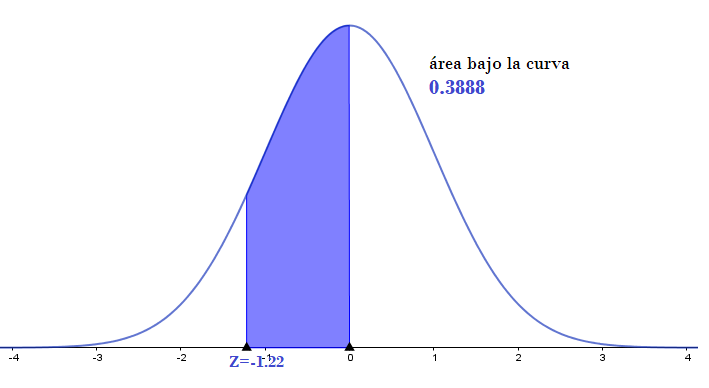
Si buscamos un valor de Z = -1.22, el área bajo la curva se puede leer en la intersección de la fila Z = 1.2 y la columna .02 (recuerda que la distribución es simétrica, el área bajo la curva de lado izquierda de la media y a la derecha de la media es de 0.5)
Elaboró: Anakaren Vega Rodríguez
La parte sombreada de la figura corresponde al área bajo la curva que se puede leer directamente en la tabla.
Elaboró: Anakaren Vega Rodríguez
Veamos el siguiente ejemplo utilizando la tabla de probabilidad:
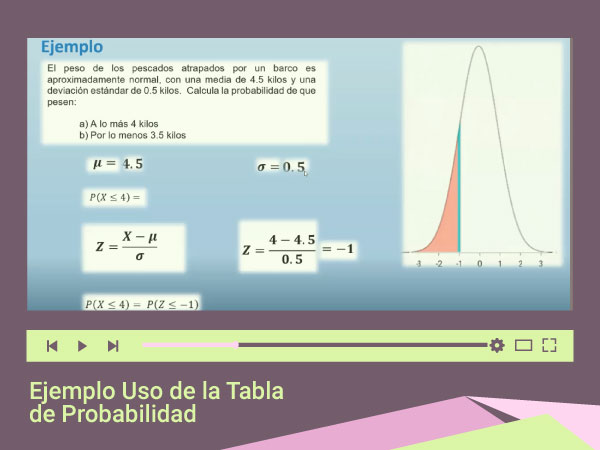
EJEMPLO: Distribución Normal con uso de tablas
A continuación será tu oportunidad de poner en práctica el cálculo de las probabilidades con la Distribución Normal.
Te acompañamos para que inicies este ejercicio y posteriormente resuelve el inciso b) y c).
Suponiendo que la distribución de las alturas de los hombres adultos es normal, con una media de 165 cm y una desviación estándar de 7 cm, encontrar la probabilidad de que un hombre adulto seleccionado al azar tenga una estatura:
- por lo menos 180 cm
- entre 180 cm y 175 cm
- a lo más 175 cm
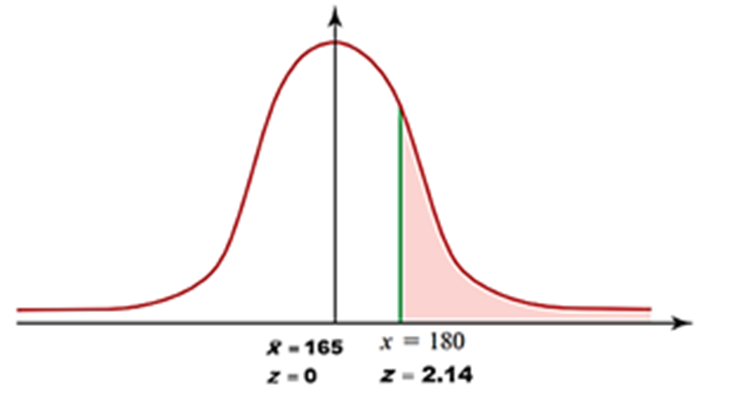
a) La probabilidad de que un hombre adulto seleccionado al azar tenga por lo menos 180 cm de estatura.
Se tiene que X = 180 cm, estandarizamos
\[z=\frac{180-165}{7}\]
\[z=\frac{15}{7}=2.14\]
Elaboró: Miguel A. Rivera Espinosa
Se busca en la tabla de probabilidad su valor
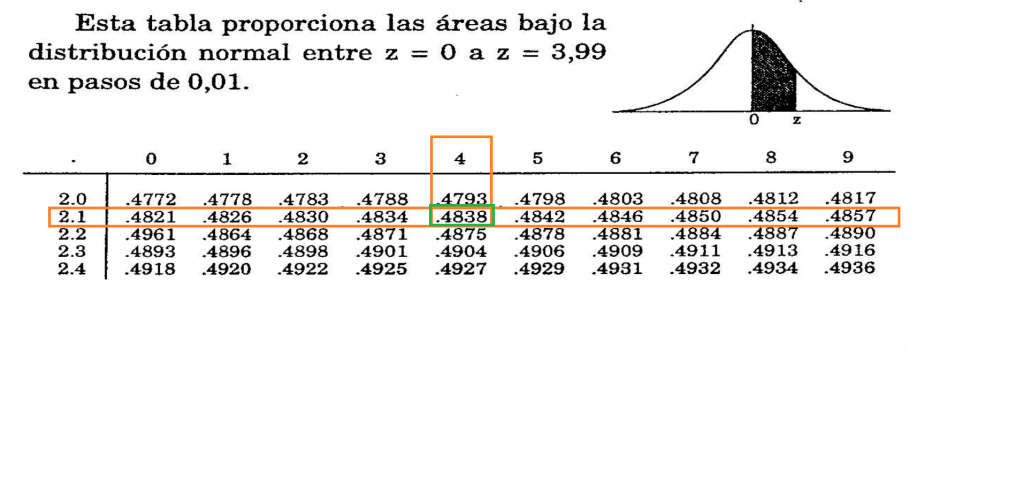
y se realiza la operación correspondiente
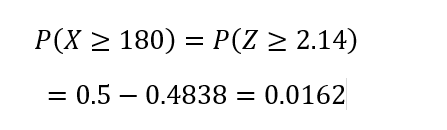
Así la probabilidad de que un adulto tenga por lo menos una estatura de 180 cm
Calculadora de Geogebra
Hasta este momento se ha visto cómo utilizar las tablas de distribución normal estándar para problemas de cálculo de áreas de distribución normal. Su uso es adecuado para los ejercicios si se cuenta con calculadora y vista la necesidad para hacer cálculos rápidos se crearon programas para ayudar con los valores de área. En está sección verán cómo obtener dichos valores con el uso de la calculadora de GeoGebra.
Ejemplo
La variable aleatoria x se distribuye de manera normal con una media de 70 y desviación estándar de 25. Calcular las siguientes probabilidades con ayuda de la calculadora de Geogebra.
- Probabilidad de que x salga con un valor menor de 60
- Probabilidad de que x salga con un valor entre 65 y 80
- Probabilidad de que x salga con un valor mayor a 62
- Probabilidad de que x salga con un valor menor a 68 y mayor a 83
Para resolver esto es necesario entrar a la calculadora de GeoGebra:
Antes que nada en la calculadora de GeoGebra se deben poner los valores de media y desviación estándar como se muestra en la imagen:
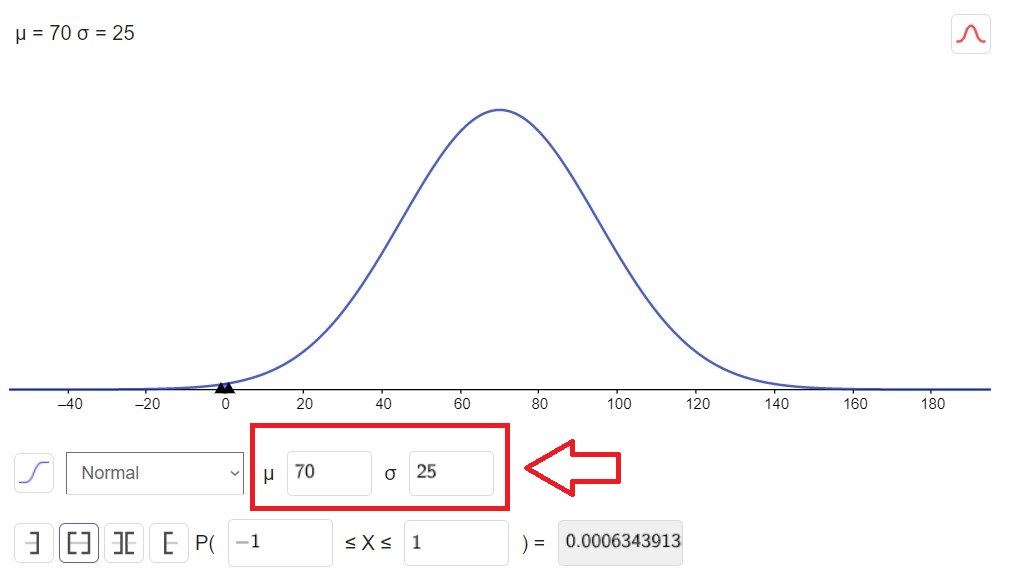
Inciso a)
Se pide la probabilidad de que x salga con un valor menor de 60, es decir: P(x<60), lo que buscamos son valores menores a cierto valor. Para ello debes usar la siguiente configuración.
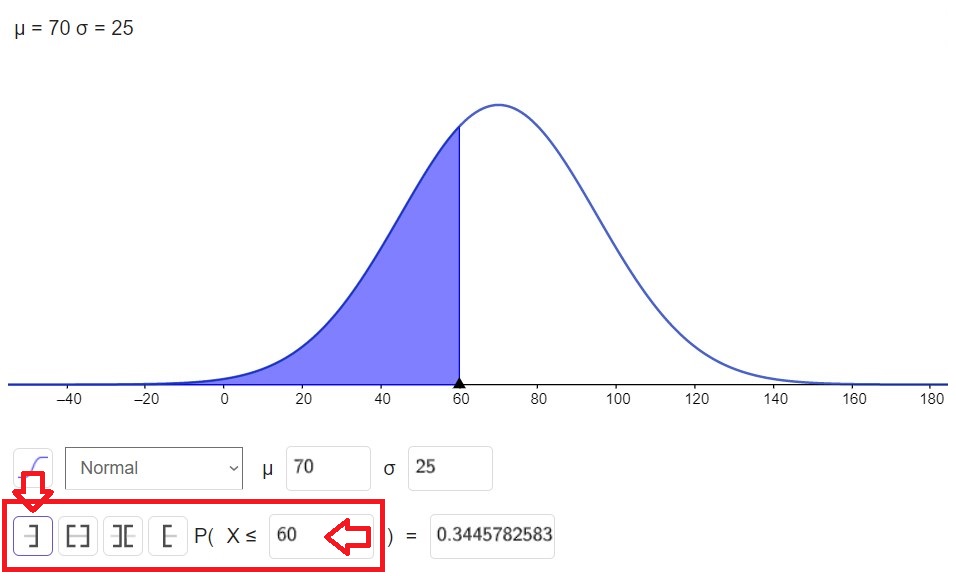
Lo cuál nos dice que la probabilidad de que nos salga un valor de x menor que 60 es de 0.3446 (Redondeado a cuatro dígitos)
Inciso b)
Probabilidad de que x salga con un valor entre 65 y 80, lo que significa que se busca el área entre dos valores, con lo cual es necesario aplicar la siguiente configuración:
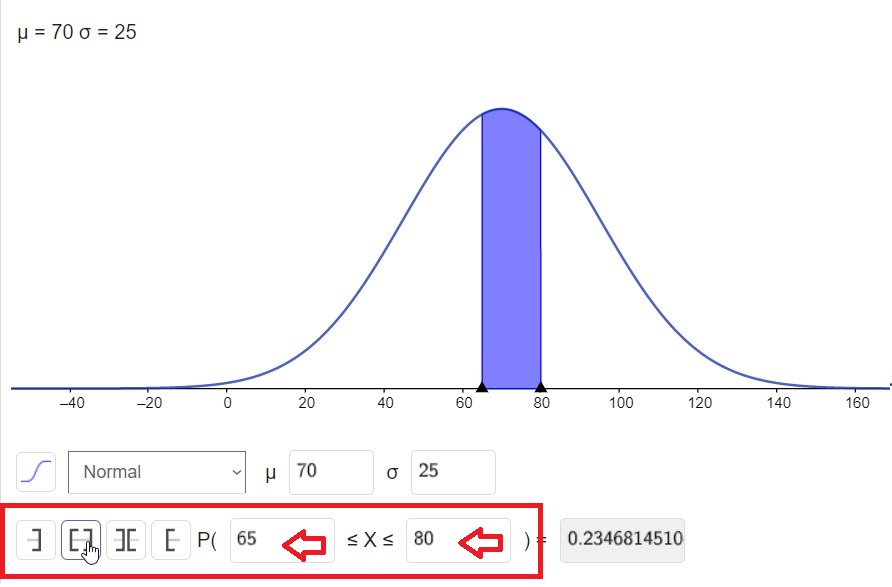
Entonces la probabilidad de que x tome un valor entre 65 y 80 es de 0.2347 (redondeado a 4 decimales).
Inciso c)
Probabilidad de que x salga con un valor mayor a 62, lo cuál nos pide el área después de un cierto valor (hasta infinito). Es necesario configurar GeoGebra de la siguiente forma.
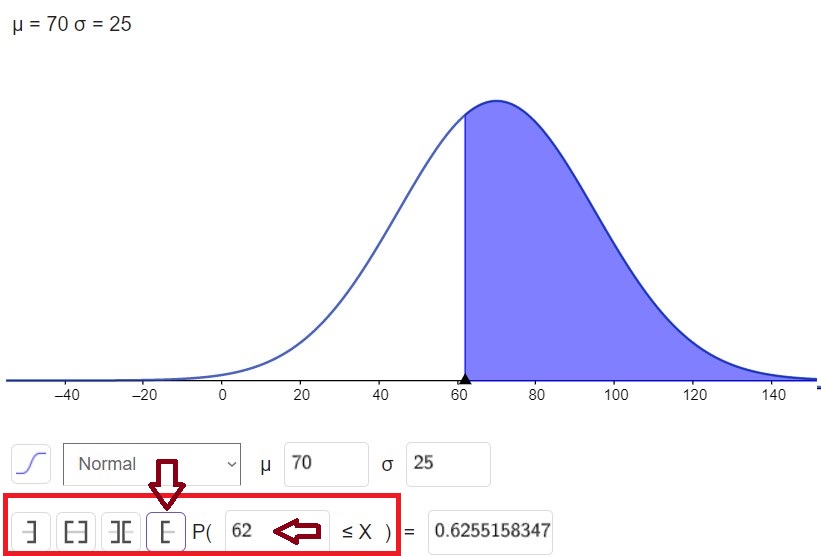
Por lo tanto, la probabilidad de que salga un valor mayor de 62 es de 0.6255 (redondeado a 4 decimales).
Inciso d)
Probabilidad de que x salga con un valor menor a 68 y mayor a 83, es decir, nos piden el área antes de un valor y después de otro valor. Para tal situación, se recomienda la siguiente configuración.
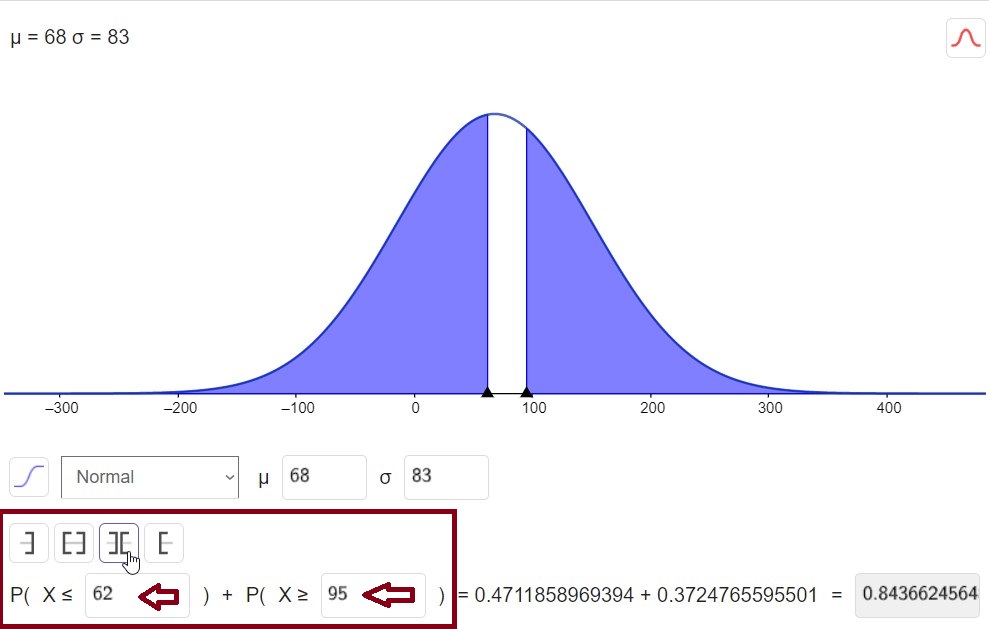
Entonces la probabilidad de que x caiga en un valor menor a 62 o mayor a 95 es de 0.8437 (redondeado a 4 decimales).