De forma similar a lo que se estudió en la congruencia, para la semejanza compararemos triángulos, por la sencillez de la figura. Para esto, ten presentes tus respuestas a las preguntas que respondiste al terminar el ejercicio anterior y la definición de semejanza, para realizar lo siguiente. Toma en cuenta los datos, no el hecho de que las figuras “parezcan” semejantes:
Determina qué parejas de triángulos son semejantes, argumenta tu respuesta y reflexiona ¿los datos proporcionados son suficientes?
a)

b)

c)
Solución
a)

Requerimos comprobar si los lados correspondientes guardan proporción, por lo que hay que identificar primero cuáles son esos lados correspondientes: Para el primer triángulo, el lado más largo es el de 15, mientras que para el segundo es el de 2.5, por tanto, es la primera pareja de lados a comparar. Para el primer triángulo, el lado más corto es el de 6, para el segundo es el de 1, por tanto, son la segunda pareja de lados a comparar. Y la tercera pareja son los lados que aún no se mencionan, el de 12 para el primer triángulo con el de 2 en el segundo triángulo.
Elegimos ahora dejar los datos del primer triángulo en el numerador y calculamos las razones:
$\frac{15}{2.5}; \frac{6}{1} ; \frac{12}{2}$
Simplificando
$\frac{15}{2.5}=6$
$\frac{6}{1}=6$
$\frac{12}{2}=6$
Las tres razones son iguales, lo cual implica que hay proporcionalidad entre las figuras con una constante de 6, es decir, los dos triángulos son semejantes: $\triangle I \sim \triangle II$
b)
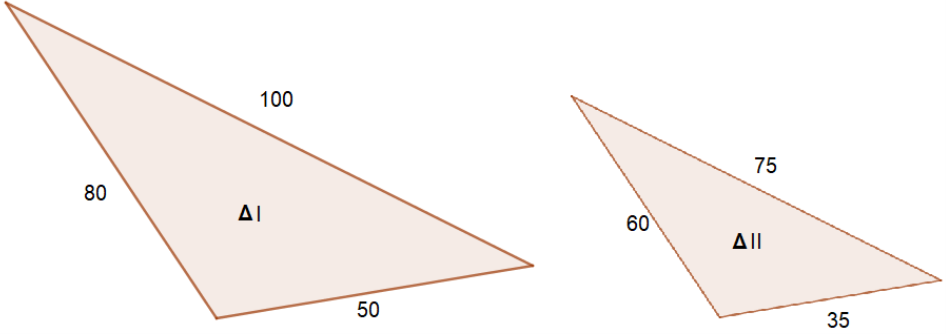
De manera similar al ejercicio anterior, comparamos los lados más largos, los lados más cortos y finalmente el tercer lado de cada triángulo, con lo que se obtienen las siguientes razones, ya simplificadas:
$\frac{100}{75}= \frac{4}{3} \approx 1.333$
$\frac{50}{35}= \frac{10}{7} \approx 1.4286$
$\frac{80}{60}= \frac{4}{3} \approx 1.333$
Observa que las razones son diferentes. A pesar de que sí haya dos iguales, el hecho de que la otra sea diferente ya implica que los dos triángulos NO son semejantes.
c) Con el apoyo de los ejemplos anteriores, verifica si la pareja de triángulos del inciso c son semejantes, después puedes verificar la solución con el botón.
Solución

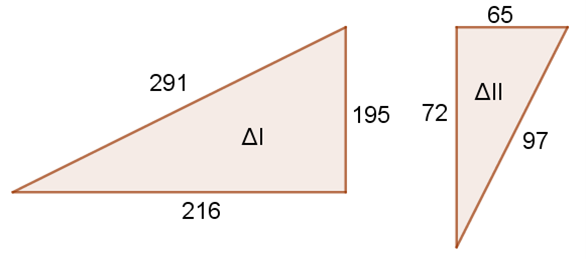
En este caso los lados más largos son 291 en el primer triángulo y 97 en el segundo. Los lados cortos son 195 y 65. Por lo tanto habría que comparar los lados de 216 y 72.
Realizando las operaciones:
$\frac{291}{97}=3$
$\frac{195}{65}=3$
$\frac{216}{72}=3$
Hay proporción, por tanto $\triangle I \sim \triangle II$
Actividad H5P
Instrucción para el alumno: ¡Es el momento de revisar lo aprendido!