Aprendizaje:
- Comprende la necesidad de medir las magnitudes identificadas. N2.
- Establece la correlación entre las variables dependiente e independiente en el estudio de un fenómeno. N2.
Las mediciones son un sello distintivo de la buena ciencia. Cuánto se sabe sobre algo a menudo está relacionado con qué tan bien se puede medir. Esto lo expresó bien el famoso físico Lord Kelvin en el siglo XIX: “Cuando uno puede medir aquello de lo que está hablando y expresarlo en números, sabe algo acerca de ello; pero cuando no puede medirlo, cuando no puede expresarlo en números, su conocimiento es escaso e insatisfactorio; podrá ser el comienzo del conocimiento, pero escasamente ha avanzado su conocimiento a la etapa de una ciencia”. Aunque puede parecer una afirmación exagerada. Las mediciones constituyen uno de los ingredientes necesarios en la experimentación. Las mediciones científicas no son algo nuevo, sino que se remontan a la antigüedad. En el siglo III aC, por ejemplo, se hicieron mediciones bastante precisas de los tamaños de la Tierra, la Luna y el Sol, y las distancias entre ellos.
Medir es comparar una magnitud con otra magnitud de referencia (patrón de referencia).
La magnitud de una cantidad física se define con un número y una unidad de medida. Ambos son necesarios porque, por sí solos, el número o la unidad carecen de significado. Las unidades de medición o patrones se eligen arbitrariamente por cada grupo social como por ejemplo la longitud del pie de un rey, la pulgada, etc. Sin embargo, el intercambio comercial y tecnológico ha impulsado a las sociedades a unificar un sistema de unidades. Revisa el siguiente vídeo “Historia del sistema internacional de unidades”

El lenguaje de la física y la tecnología es universal, es decir que, las magnitudes deben expresarse de una manera precisa y consistente, de manera que un término determinado signifique exactamente lo mismo para todos.
En la actualidad todas las unidades fundamentales o básicas del SI están definidas en términos de experimentos físicos que pueden efectuarse en laboratorios en cualquier lugar del mundo sin recurrir al prototipo patrón. Revisa la siguiente tabla de unidades fundamentales.
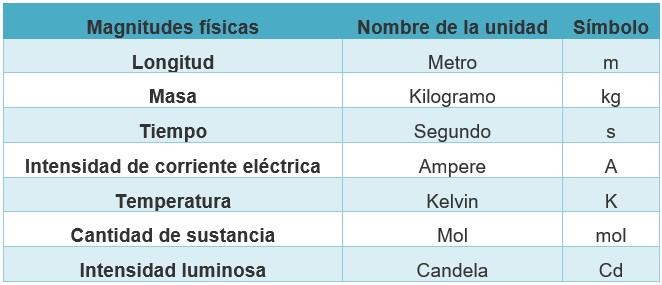
El SI es un sistema coherente, ya que el producto o el cociente de dos o más de sus magnitudes dan como resultado la unidad derivada correspondiente. Por ejemplo: la unidad de fuerza (N), se obtiene al multiplicar la unidad de masa (kg) por la unidad de aceleración (m/s2), por tanto: N = kg m/s2. Revisa la siguiente tabla de algunas unidades derivadas, ya que se obtienen de productos o cocientes de otras unidades.
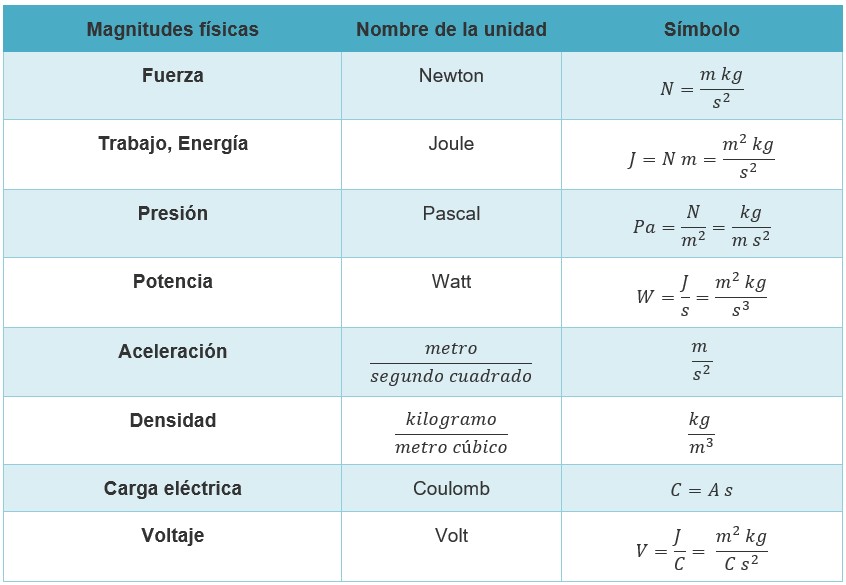
Adicionalmente el SI tiene la ventaja de que utiliza exclusivamente el sistema arábigo de numeración con base 10, lo cual permite que los múltiplos y submúltiplos tengan relaciones decimales con la unidad. Es decir, se pueden utilizar prefijos antes de la unidad para facilitar el trabajo con las magnitudes SI demasiado grandes o pequeñas. Por ejemplo el prefijo kilo que antecede a la unidad metro es igual a 1000 metros: km = 1000 m. Revisa la tabla de algunos prefijos del SI, supongo que te recordarán términos utilizados en la actualidad como en el almacenamiento de datos en discos de Terabytes.
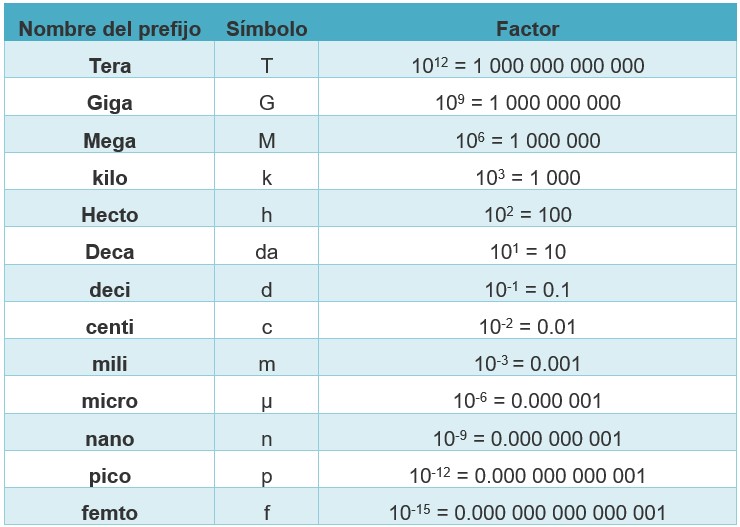
Como comentamos antes, para describir un sistema o fenómeno físico utilizamos modelos matemáticos (ecuaciones), pero ¿cómo se obtienen estos modelos?
Regresemos un poco, como resultado de la observación de un fenómeno surge la pregunta: ¿qué causa ese fenómeno?, se identifican las variables involucradas y se intenta encontrar la relación entre estas para responder la pregunta. Una forma muy común es analizar los cambios de las variables independiente y dependiente obtenidos con la experimentación, normalmente se obtienen tablas con las magnitudes de ambas variables, pero es muy difícil visualizar el comportamiento de las variables a partir de las tablas. Para analizar el comportamiento de las variables se grafican, la variable independiente en el eje de las x’s y la variable dependiente el en eje de las y`s. Una simple gráfica comprenderá toda la información y facilitará la apreciación visual de los resultados del experimento.
De la interpretación de la gráfica se puede tener un modelo empírico válido en el intervalo de valores experimentado. En la tabla se muestran algunas de las correlaciones más frecuentes entre variables. La correlación es una medida de la relación (covariación) entre dos variables cuantitativas contínuas (x, y). La manera más sencilla de saber si dos variables están correlacionadas es determinar si co-varían (varían conjuntamente). Así, la correlación es útil para describir relaciones simples entre datos o variables. Por ejemplo, en un experimento de un circuito eléctrico que cuenta con una batería y un resistor, queremos saber cómo cambia el voltaje y la corriente del circuito y, si están correlacionados.
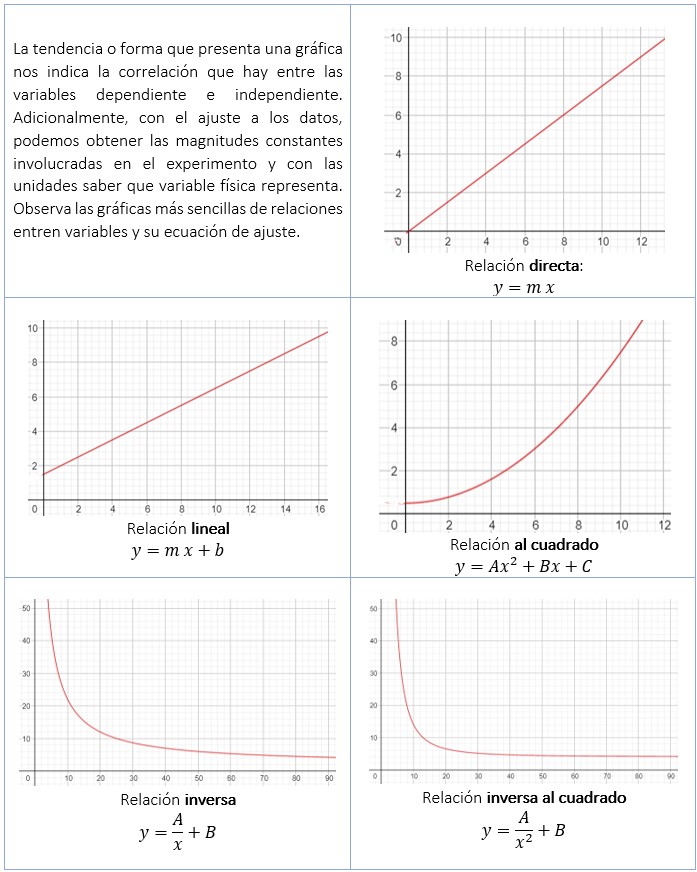
Así entonces, podemos obtener un modelo graficando los cambios entre las variables del experimento y analizando su comportamiento.
Actividad H5P
Instrucción para el alumno: ¡Es el momento de revisar lo aprendido!