Distribución de probabilidad de una variable aleatoria discreta en una Máquina de Galton
En está parte podrás crear una distribución de probabilidad teórica y experimental para alguna configuración de la máquina de Galton usando un simulador de este genial invento.
Originalmente la máquina de Galton fue creada por Francis Galton para demostrar el teorema del límite central. Dicho teorema se verá más adelante; lo que nos interesa de este invento es la forma en que se distribuyen las bolitas, ya que podríamos calcular qué tan probable es que caiga en los diferentes compartimentos como se puede ver en el siguiente vídeo.

Ahora que viste el vídeo podrás notar que las bolitas se acumulan más en los compartimentos centrales, sin embargo, ¿Por qué crees que pasa eso? Para resolver esta incógnita hay que suponer algunas cosas, como que al momento de pasar una bolita por cada clavo tiene la misma probabilidad de irse a la izquierda o a la derecha, es decir, una probabilidad de cada lado de 0.5 y 0.5 respectivamente. Además de que esto va a ocurrir en cada fila de clavos.
Abre el siguiente simulador para familiarizarte con lo que pasa en esta máquina de Galton. Explora y juega con las diferentes configuraciones del simulador tanto en la sección de Intro y Laboratorio. ¿Puedes cambiar el número de filas que hay?, ¿Puedes tirar una bolita o más?, ¿Puedes ver los caminos que recorre cada pelotita? Intenta averiguar todo lo que el simulador ofrece. Una vez termines, vuelve a está pantalla.

Ejemplo 1
Para este primer ejemplo analizaremos una configuración sencilla de la máquina de Galton. Para ello abre el simulador de la máquina de Galton, entra en la sección Laboratorio y coloca la configuración. Una vez hecho esto, sigue las instrucciones.
- Dos filas de clavos
- Mismas probabilidades para donde vaya la bolita en los clavos.

Elaboró: Ing. Moisés Amadeus Mejía Rivera
Usando el botón de acción verde podemos ver como caen las bolitas y que en cada ocasión toman un camino diferente. Para ver las trayectorias, basta con seleccionar la opción “Camino”. De tal forma que se observan los siguientes caminos a los diferentes compartimentos:
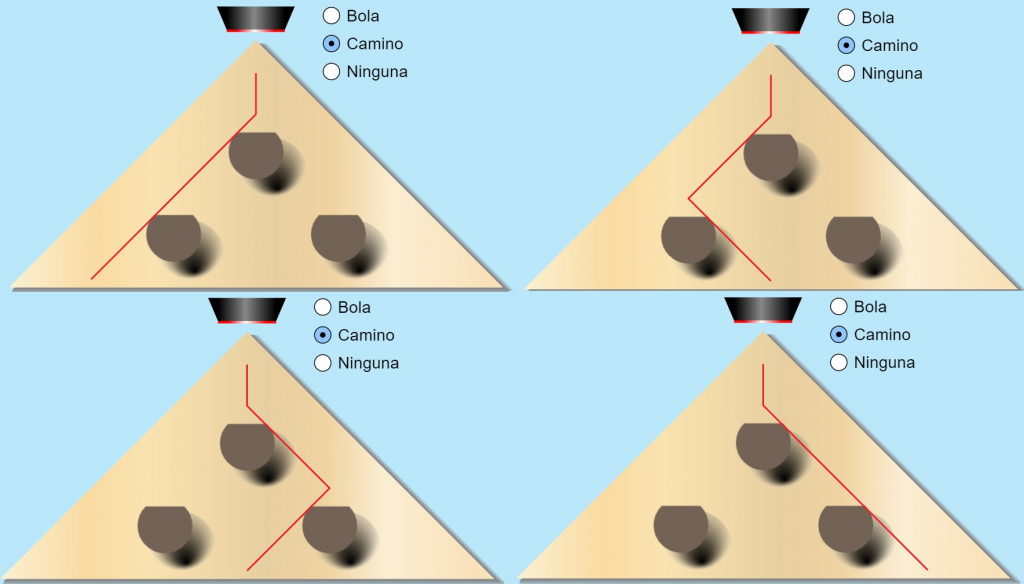
Elaboró: Moisés Amadeus Mejía Rivera
Observando los resultados, se obtienen los caminos posibles para cada uno de los compartimentos:
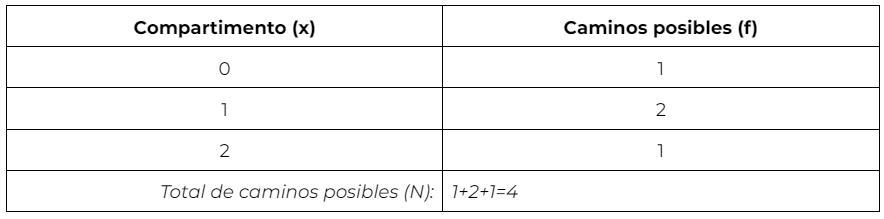
Al saber los caminos posibles y el total, se puede calcular de manera teórica la distribución de probabilidades según su compartimento con el uso de la probabilidad clásica:
| $P\left(x\right)=\frac{f}{N}$ La probabilidad de que la bolita caiga en el compartimento x es igual a la división del número de caminos posibles para llegar al compartimento x (f) entre el número total de trayectorias (n). |
Con lo que queda la siguiente distribución de probabilidades:

Lo que nos da la tabla anterior es la probabilidad de que una bolita en un ensayo caiga en cada uno de los compartimentos. Por ejemplo, la probabilidad más alta en que caiga una bolita es en el compartimento 1 con una probabilidad de 0.5. Dicha probabilidad es porque solo se puede llegar al compartimento 1 por dos caminos de los cuatro posibles.
Y… ¿Qué pasa con la distribución de las bolitas cuando se tiran 1, 10, 100, 1000 o más bolitas? ¿La probabilidad frecuencial se parecerá a la probabilidad teórica? Veamos qué pasa.
Abre de nuevo el simulador con la misma configuración y observa lo que pasa con más de 1000 ensayos (N>1000).
En está simulación realizada salió las siguientes probabilidades frecuenciales:
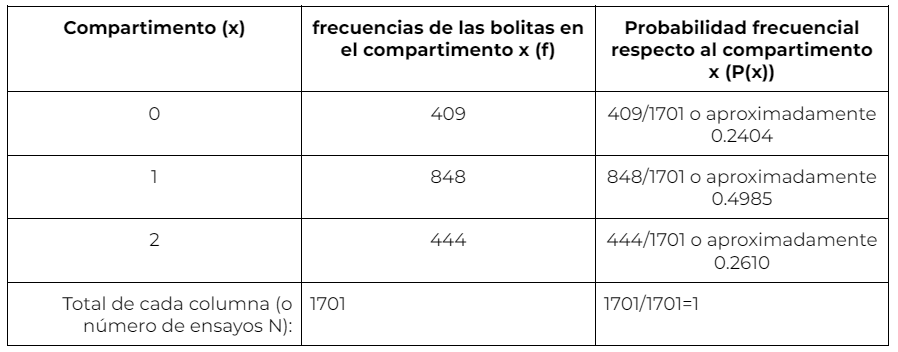
Analizando la tabla y comparando con las probabilidades teóricas se puede observar que se acercan mucho las probabilidades frecuenciales. Y se sabe que mientras más ensayos se hagan, las probabilidades frecuenciales se acercarán más a las probabilidades teóricas.
Ojo, ¡no somos adivinos!, ya que no podemos saber dónde caerá la próxima bolita, sin embargo sí se puede saber que probabilidades hay de que caiga en cada compartimento y si hablamos de muchos ensayos, es posible saber a la larga cómo se distribuirán de forma aproximada las bolitas de acuerdo a su probabilidad teórica. Para esto es que nos sirve saber las probabilidades teóricas y su comprobación en los experimentos.
¡Es el momento de revisar lo aprendido!