Variable Aleatoria
Las Variables Aleatorias que se observan en la naturaleza poseen ciertas características y se pueden clasificar según su tipo. Por ejemplo: el número de insectos que se mueren al aplicar una dosis de insecticida, suponiendo que sólo estamos interesados en el número de insectos muertos. Entonces los resultados pueden representarse por los números 0, 1, 2, 3,…n.
Si consideramos esos números como valores tomados por una variable X, entonces esa variable toma valores de acuerdo con los resultados de un experimento aleatorio, y podemos pensar en X como en una variable aleatoria, que en este caso representa el número de insectos muertos.
La Variable aleatoria asume un valor numérico único para cada uno de los resultados que aparecen en el espacio muestral de un experimento de probabilidad. Dicho de otra manera, la variable aleatoria es una función que asocia un número real con cada elemento del espacio muestral.
Para comprender mejor esto te invitamos a ver el siguiente video

Trabajemos con otro ejemplo en el siguiente video
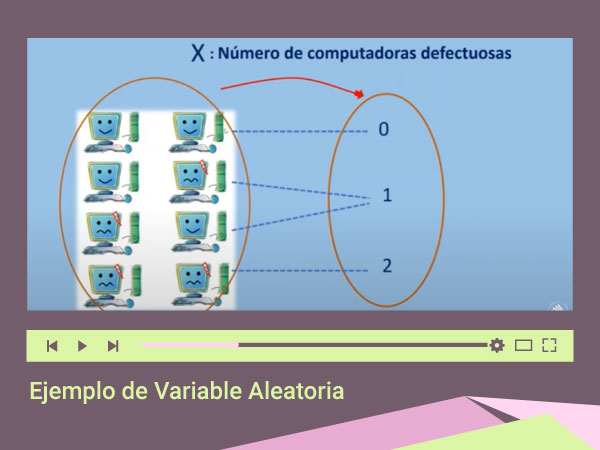
Las variables aleatorias numéricas pueden subdividirse en dos clases: Variables Aleatorias Discretas y Variables Aleatorias Continuas.
Variable Aleatoria Discreta
Un concepto de variable aleatoria discreta es el siguiente:
“Una variable aleatoria discreta tiene un número finito de valores o un número de valores contable, donde contable se refiere al hecho de que podría haber un número infinito de valores, pero que pueden asociarse con un proceso de conteo, de manera que el número de valores es 0 o 1 o 2 o 3 etcétera ” (Triola, 2013)
Para que quede más claro te presentamos el siguiente vídeo, en el cual se explica el concepto de variable aleatoria discreta con algunos ejemplos.

Referencia:
Triola, M. F., Pineda Ayala, L. E., & Triola, M. F. (2013). Estadística (Decimoprimera edición). Pearson.
Variable Aleatoria Discreta, Ejercicio Autocompartido
Autocompartido.com
¡Comparte el viaje de la vida!
Los pueblos y ciudades de todo el país están atascados con el tráfico: muchos de estos automóviles tienen un solo ocupante.

Pexels.
Para resolver este problema, Autocompartido.com está lanzando un nuevo esquema para que las personas compartan automóviles en viajes a las principales ciudades.
Nuestra completa base de datos puede poner a los conductores interesados en contacto entre sí y las actualizaciones en tiempo real a través de su celular mostrarán la cantidad de automóviles compartidos disponibles en cualquier ciudad importante.
Los coches compartidos están disponibles en ubicaciones centralizadas para una máxima comodidad.
Autocompartido.com está ejecutando un pequeño plan de prueba en una ciudad concurrida en el sur de México. Realizaremos una encuesta para medir el éxito del ensayo. Manténgase al día con la prueba a través de las últimas noticias en nuestro sitio web.
¿Cómo recopilar información sobre el volumen de tráfico en la ciudad?
Se realizó un estudio de tráfico, en puntos críticos alrededor del centro de la ciudad, en las horas pico de viaje durante un período de una semana laboral. La encuesta involucró a 1000 autos. Se anotó el número de personas en cada automóvil, con los siguientes resultados.
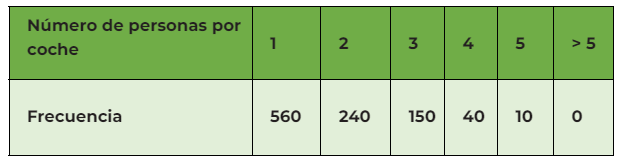
[?] ¿Cuáles son las principales características de esta distribución?
El número de personas por coche es necesariamente discreto. Una distribución de frecuencia discreta se ilustra mejor con un gráfico de barras, como en la figura 1. Esto muestra que la distribución tiene un sesgo positivo, con la mayoría de los datos en el extremo inferior de la distribución.
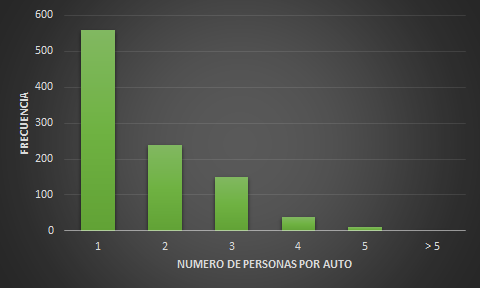
FIGURA 1.- Distribución de frecuencias para el caso del número de personas por auto,
elaborado por Miguel A. Rivera en Excel
Ahora tiene un modelo matemático para describir una situación particular. En las estadísticas, a menudo busca modelos para describir y explicar los datos que encuentra en el mundo real. En esta lección se presentan algunas de las técnicas para trabajar con modelos para datos discretos. Tales modelos utilizan variables aleatorias discretas.
El modelo es discreto ya que el número de pasajeros se puede contar y solo toma valores enteros positivos. El número de pasajeros es una variable aleatoria ya que el valor real del resultado es variable y solo se puede predecir con una probabilidad dada, es decir, los resultados ocurren al azar.
Las variables aleatorias discretas pueden tener un número finito o infinito de resultados.
La distribución que hemos esbozado hasta ahora es finita: en la encuesta, el número máximo de personas observadas fue de cinco, pero el máximo podría ser, digamos, ocho, dependiendo del tamaño del automóvil. En este caso habría ocho resultados posibles. Un ejemplo bien conocido de una variable aleatoria discreta finita es la distribución binomial, que se verá en la siguiente unidad.
Una variable aleatoria discreta generalmente se denota con una letra mayúscula, como X, a Z. Puedes pensar en esto como el nombre de la variable. Los valores particulares que toma la variable se denotan con letras minúsculas, como r. A veces a estos se les dan sufijos r1, r2, r3, … . Así P(X = r1) significa la probabilidad de que la variable aleatoria discreta X tome un valor particular r1. La expresión P(X = r) se utiliza para expresar una idea más general, como por ejemplo, en un encabezado de tabla.
Otra forma más corta de escribir probabilidades es p1, p2,p3, … . Si una variable aleatoria discreta finita tiene “n” resultados distintos r1, r2,…, rn, con probabilidades asociadas p1, p2, …, pn, entonces la suma de las probabilidades debe ser igual a 1. Dado que los diversos resultados cubren todas las posibilidades, son exhaustivos.
Formalmente tenemos:
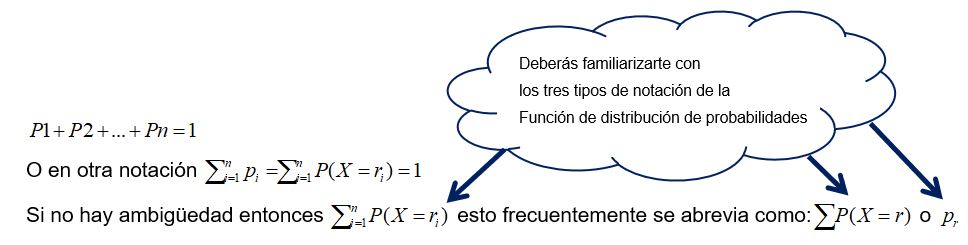
Elaboró: Miguel A. Rivera Espinosa
Diagramas de variables aleatorias discretas
Al igual que con las distribuciones de frecuencia para datos discretos, el diagrama más apropiado para ilustrar una variable aleatoria discreta es un gráfico de líneas barras. La Figura 2 muestra un diagrama de la distribución de probabilidad de X, el número de personas por automóvil. Ten en cuenta que es idéntico en forma al diagrama de frecuencia correspondiente en la figura 1. La única diferencia real es el cambio de escala en el eje vertical.
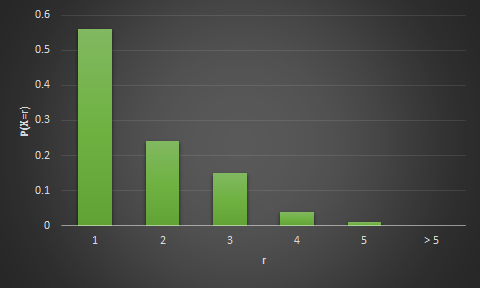
Figura 2.- Diagrama de Distribución de probabilidades de X,
elaborado por Miguel A. Rivera en Excel
Variable Aleatoria Discreta, ejemplo dados tetraédricos
EJEMPLO
Se lanzan dos dados tetraédricos, cada uno con caras etiquetadas como 1, 2, 3 y 4, y la variable aleatoria X representa la suma de los números que se muestran en los dados.
(i) Encuentra la distribución de probabilidad de X.
(ii) Ilustrar la distribución y describir la forma de la distribución.(iii) ¿Cuál es la probabilidad de que cualquier lanzamiento de dados resulte en un valor de X que es un número impar?
SOLUCIÓN(i) La tabla muestra todos los totales posibles cuando se lanzan los dos dados.
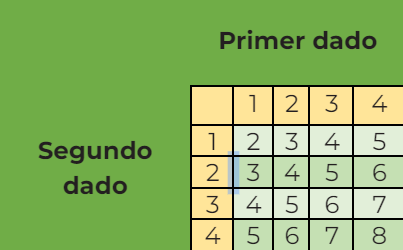
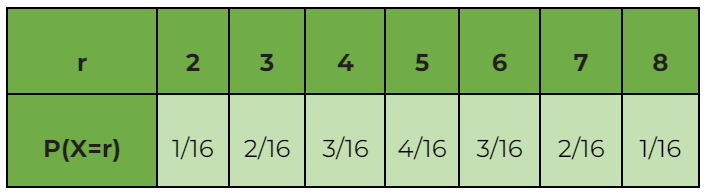
Puedes usar la tabla para anotar la distribución de probabilidad para X.
(ii) El gráfico de barras de la figura 3 ilustra esta distribución, que es “simétrica”.
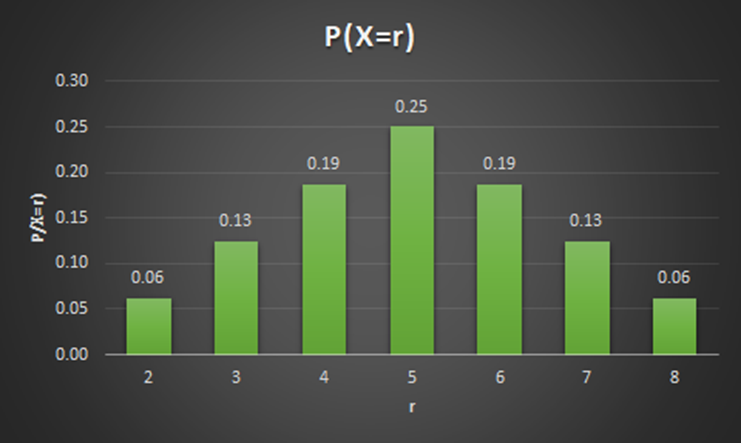
Figura 3 Distribución de probabilidades, de tipo simétrico y discreto
elaborado por Miguel A. Rivera en Excel
(iii) La probabilidad de que X sea un número impar
P(X = 3) + P(X = 5) + P(X = 7) =2/16+4/16+2/16
=1/2
Variable Aleatoria Continua Definición
No todas las mediciones de variables aleatorias son del tipo discreto; por ejemplo, medir el tiempo de llegada al CCH, el peso y la estatura de los alumnos que toman educación física, etc. Por ejemplo, una medición del peso de una alumna puede ser entre 40 y 41 kg, tal como 40.360kg. En este caso la única limitante entre un valor y otro es la precisión del instrumento, que puede ser de 0.01kg y por tanto la medidas intermedias entre 40 y 41 kg, podrían ser: 40.01, 40.02, 40.03 kg y así sucesivamente hasta llegar a 40.98, 40.99 y finalmente 41.00 kg, en caso de que la precisión del instrumento de medición sea 0.001 kg, algunas mediciones entre 40.000 y 41.000 kg podrían ser: 40.456, 40.365, 40.750, 40.999 hasta 41.000kg. Por lo tanto no existe limitante desde el punto de vista matemático entre un intervalo dado de valores, es decir, que dentro del intervalo [40… 41] pueden existir infinitos valores, de modo que la variable del peso no es de tipo contable o discreto, sino INFINITOS VALORES. A este tipo de variables aleatorias se les llama variables aleatorias de tipo CONTINUO.
En el siguiente video se explica lo anterior:

A las variables aleatorias de este tipo como el peso, la estatura o el tiempo de llegada a la escuela se les llama variable aleatoria de tipo CONTINUA, en donde los valores posibles forman un intervalo infinito, es decir, continuo y las probabilidades asociadas a este tipo de variables solo se asocian a este intervalo y no con valores individuales, sino con valores innumerables.
Las típicas variables continuas miden alguna cantidad, como las anteriores: peso, volumen, presión arterial, la concentración de químicos en la sangre, etc. Ejemplo de Variables aleatorias continuas serían:
- El tiempo entre llamadas de celular
- El peso de la proteína en una torta
- La resistencia eléctrica de un LED
- El volumen de contenido de un refresco
- La temperatura de un horno
Esta misma explicación respecto a varios tipos de variables aleatorias de tipo continuo, se puede ver en el siguiente video:

Referencias de esta pantalla: Domínguez, D. J., & Domínguez, L. J. A. (2006). Estadística y probabilidad: El mundo de los datos y el azar. México, D.F: Oxford University.
¡Es el momento de revisar lo aprendido!