Un estadístico muy importante para el estudio de datos estadísticos bivariados es el coeficiente de correlación lineal o coeficiente momento de producto de Pearson, el cual mide el grado de dependencia lineal entre las dos variables ($x$ e $y$). El símbolo que se utiliza para el parámetro es $\rho$ (letra griega rho) y para el estadístico la letra $r$.
Este coeficiente siempre toma un valor numérico entre –1 y +1 y mide la intensidad de la relación lineal entre dos variables cuantitativas. Cuando $r$ es negativo y tiene un valor cercano a –1, indica que hay una dependencia lineal negativa entre las variables, indicando que si $x$ aumenta, $y$ disminuye o si $x$ disminuye, $y$ aumenta. Cuando $r$ es positivo y tiene un valor cercano a 1, se tendrá que las variables son linealmente dependientes positivamente, lo cual significa que si $x$ aumenta, $y$ aumenta y viceversa. Si $r=0$ o es un valor cercano a cero, se concluye que hay muy poca o ninguna correlación lineal, las variables son linealmente independientes.
Una correlación de +1 indica una dependencia lineal perfecta y un valor de –1 habla de una relación negativa óptima, y todos los puntos $(x, y)$ están exactamente en una recta, pero estos valores rara vez aparecen en situaciones reales.
Para obtener el coeficiente de correlación lineal se usa la fórmula:
\[r = \frac{\sum_{=1}^{n}\left ( x_{i} – \bar{X} \right )\left ( y_{i} – \bar{Y} \right )}{\sqrt{\left [ \sum_{i=1}^{n}\left ( x_{i} – \bar{X} \right )^{2} \right ]\left [ \sum_{i=1}^{n}\left ( y_{i}- \bar{Y} \right )^{2} \right ]}}\]
donde $\bar{X}$ = media aritmética de la variable $x$
$\bar{Y}$ = media aritmética de la variable $y$
$n$ = número de observaciones o datos.
El coeficiente de correlación tiene su principal uso en la Regresión Lineal, para ajustar los valores bivariados a una recta lineal.
Ejemplo:
Tomando los datos de la tabla anterior (precios promedio y tamaños de pantallas Smart TV), se calculará el coeficiente de correlación para determinar si existe dependencia lineal o no entre las variables.
Como ya se señaló la variable $x$ es el tamaño de la pantalla y el precio la variable $y$, porque el precio depende del tamaño de la pantalla, a continuación se obtienen las medias aritméticas de los valores y las sumas que se indican en la fórmula.
El tamaño promedio de las pantallas es de aproximadamente 49.77 pulgadas, dado que:
$\bar{X}=\frac{3(32)+40+5(43)+49+3(50)+4(55)+60+3(65)+70}{22}=49.7727$
El precio promedio de las pantallas es de aproximadamente $11, 617.42, ya que se obtiene de la forma siguiente:
$\bar{Y}=\frac{8183+9681.85+8500.38+\cdots+5356.18}{22}=11617.4232$
Las sumas indicadas
$\sqrt{\sum_{i=1}^{n}\left ( x_{i}-49.77 \right )^2} = \sqrt{3\left ( 32-49.77 \right )^2+\left ( 40-49.77 \right )^2+5\left ( 43-49.77 \right )^2 + \cdots \left ( 70-49.77 \right )^2} = \sqrt{2591.86} = 50.91$
$\sqrt{\sum_{i=1}^{n}\left ( y_{i}-11617.42 \right )^2} = \sqrt{\left ( 8183-11617.42 \right )^2+\left ( 9681.85-11617.42 \right )^2+\left ( 8500.38-11617.42 \right )^2 + \cdots \left ( 5356.18-11617.42 \right )^2} = \sqrt{330977768.79} = 18192.79$
$\sum_{i=1}^{n}\left ( x_{i}-49.77 \right )\left ( y_{i}-11617.42 \right ) = \left ( 40-49.77 \right )\left ( 8183-11617.42 \right )+\left ( 43-49.77 \right )\left ( 9681.85-11617.42 \right )+ \cdots +\left ( 32-49.77 \right )\left ( 5356.18-11617.42 \right ) = 872313.95$
Los anteriores cálculos se pueden apreciar en la tabla siguiente:
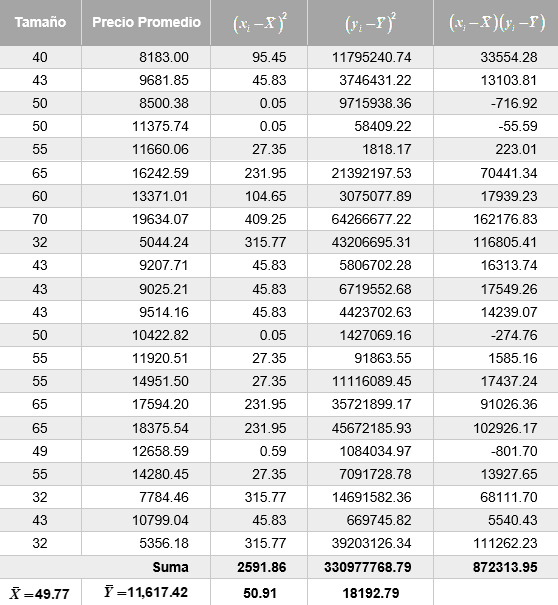
Por consiguiente, el coeficiente momento producto de Pearson es igual a:
$r = \frac{872313.95}{50.91\left (18192.79 \right )} = 0.9418$, es cual es un valor muy cercano a uno.
Lo anterior significa, las variables tienen una correlación lineal positiva, es decir, que el precio de una pantalla depende de su tamaño. A mayor tamaño de la pantalla, mayor será el precio y viceversa.
Enseguida se procederá determinar cómo se estima la línea de mejor ajuste para un conjunto de datos bivariados.