Este teorema se utiliza en distintas áreas y establece la relación entre los lados de un triángulo rectángulo, recuerda que estos tienen un ángulo recto, es decir un ángulo de 90° y dos ángulos agudos. Debes considerar que en un triángulo rectángulo, el lado situado frente al ángulo recto corresponde a la hipotenusa, mientras que los lados situados frente a los ángulos agudos se conocen como catetos, observa la siguiente figura:
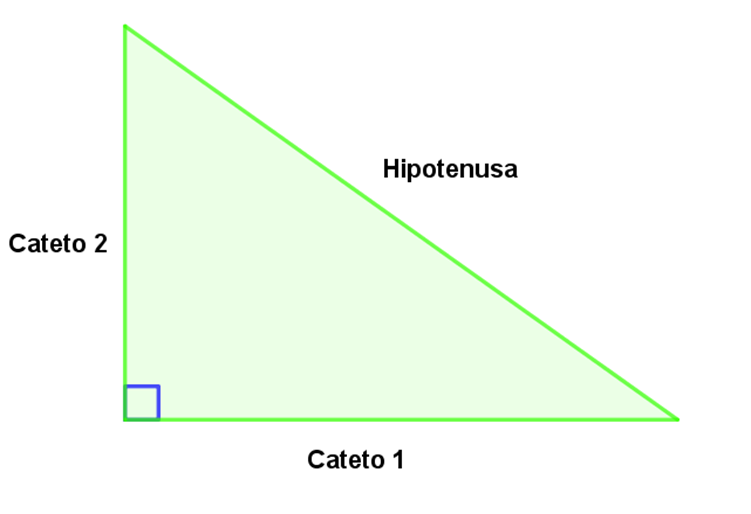
El teorema de Pitágoras establece que, en un triángulo rectángulo, la suma del cuadrado de los catetos $a$ y $b$ es igual al cuadrado de la hipotenusa $c$, es decir:
\[a^2+b^2=c^2\]
Este teorema lo podemos emplear cuando se conocen dos lados de un triángulo rectángulo, es decir, si se conocen los dos catetos, o bien, la hipotenusa y uno de sus catetos, y el tercer lado del triángulo se puede obtener al sustituir en la expresión $a^2+b^2=c^2$ o en caso de ser necesario, despejando a alguno de los catetos.
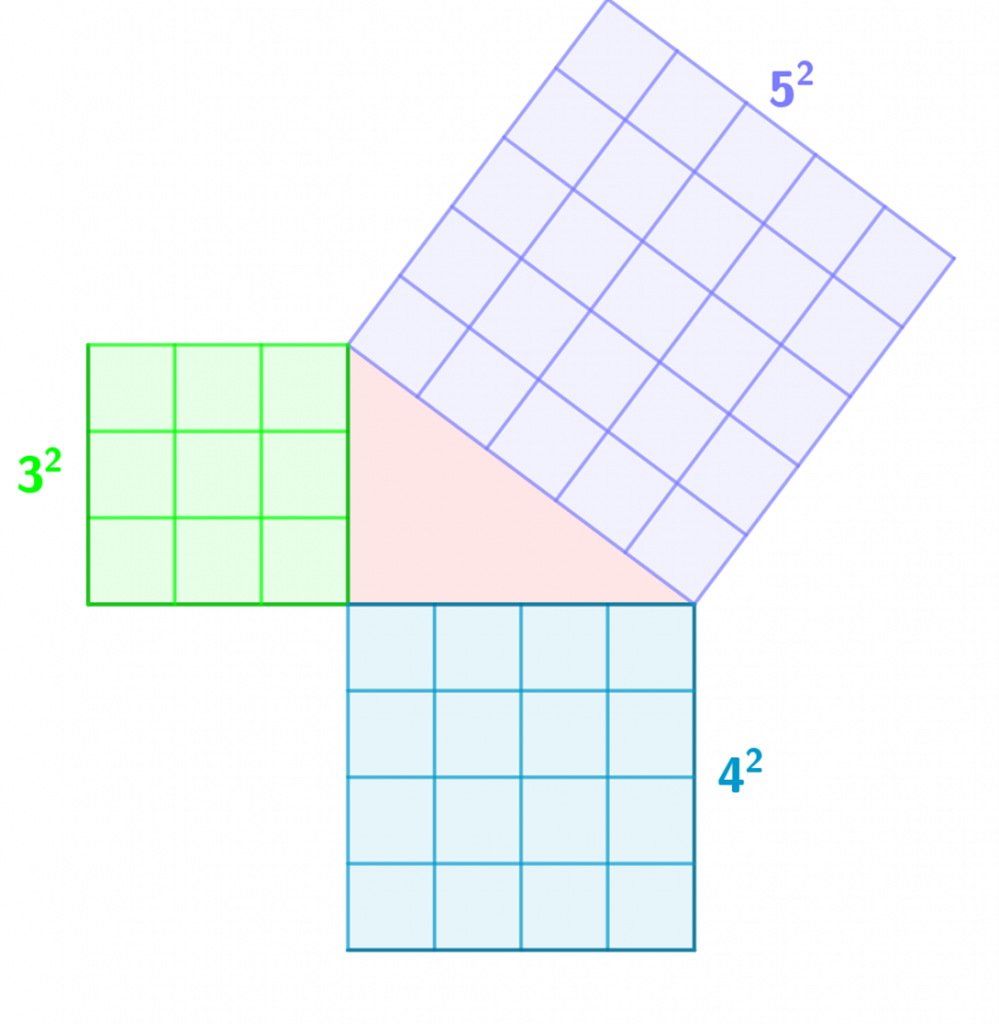
En esta figura se están dibujando cuadrados cuyos lados coinciden con la longitud de los lados del triángulo, en donde se puede visualizar el área de estos, y verificar que la suma del cuadrado de los catetos corresponde al cuadrado de la hipotenusa, es decir:
\[3^2+4^2=5^2\]
\[9+16=25\]
\[25=25\]
Con lo que se comprueba el teorema.
Revisa los siguientes ejemplos que se despliegan al dar clic sobre los mismos:
Ejemplo 1. Obtener la medida del lado faltante en la siguiente figura:
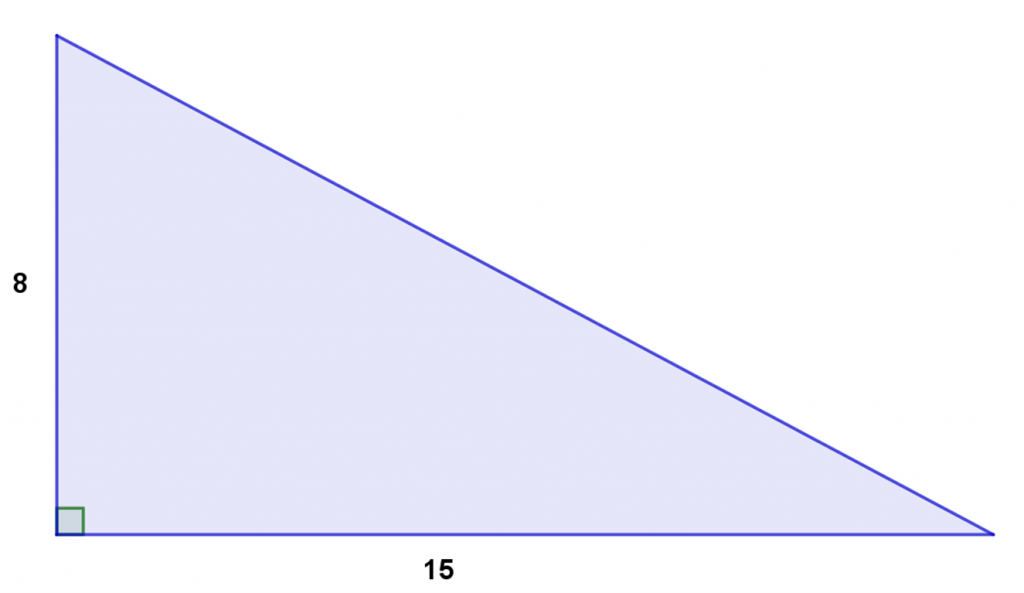
Como se observa en la figura, el lado faltante corresponde a la hipotenusa, por lo que aplicando el Teorema de Pitágoras, tenemos:
\[8^2+15^2=c^2\]
\[64+225=c^2\]
\[289=c^2\]
Despejando a la hipotenusa, tenemos:
.\[c=\sqrt{289}\]
\[c=17\]
Ejemplo 2. Obtener la medida del lado faltante en la siguiente figura:
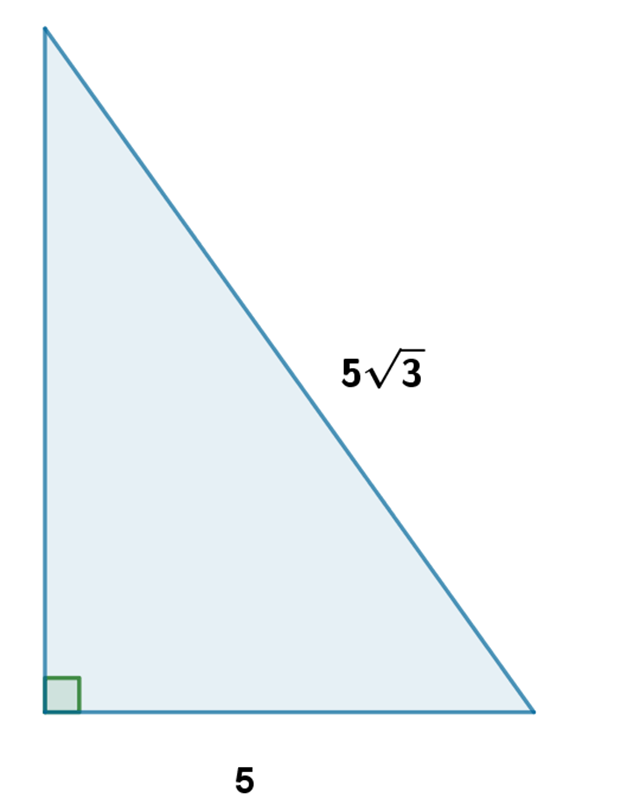
Como se observa en la figura, el lado faltante corresponde a uno de los catetos, por lo que aplicando el Teorema de Pitágoras, tenemos:
\[a^2+5^2=\left ( 5\sqrt{3} \right )^2\]
\[a^2+5^2=\left ( 5 \right )^2\left ( \sqrt{3} \right )^2\]
\[a^2+25=\left ( 25 \right )\left ( 3\right )\]
\[a^2+25=75\]
Despejando al cateto \[a\], tenemos:
.\[a=\sqrt{75-25}\]
\[a=\sqrt{50}\]
Simplificando la raíz
\[a=\sqrt{25\left ( 2 \right )}=\sqrt{25}\sqrt{2}=5\sqrt{2}\]
Por lo que el lado faltante mide:
\[a=5\sqrt{2}\]
El teorema de Pitágoras tiene aplicaciones en situaciones reales, estos son algunos ejemplos:
Arquitectura: en construcciones con techos triangulares y hastiales

Navegación: para la localización de objetos con base en dos puntos de referencia se usa la triangulación, los servicios de geolocalización por GPS usan este método.
Localización de terremotos: para ubicar el epicentro de un terremoto, los geólogos triangulan la distancia que recorre la onda más rápida con la que recorre la onda más lenta.
Revisa la siguiente aplicación del teorema de Pitágoras:
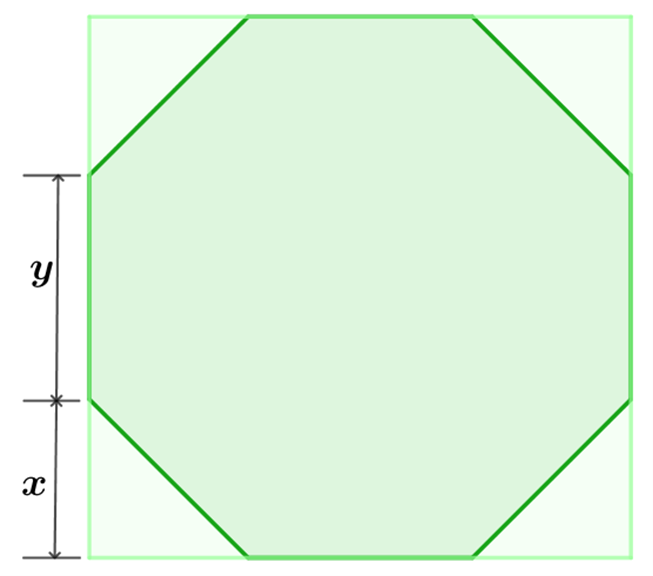
A partir de un cuadrado se forma un octágono regular cortando un triángulo rectángulo isósceles de cada esquina. Si cada lado del cuadrado mide 20 cm, ¿cuánto mide cada lado del octágono?
Solución.
Como se observa en la imagen, los lados iguales de los triángulos isósceles miden x, mientras que el lado desigual y, este último corresponde a los lados del octágono.
Por lo anterior, los lados del cuadrado se pueden definir como:
\[2x+y=20 … ecuación \ 1 \]
Por teorema de Pitágoras, en el triángulo isósceles tenemos:
\[x^2+x^2=y^2\]
\[2x^2=y^2\]
Despejando a $y$
\[y=\sqrt{2x^2}\]
\[y=\sqrt{2} x … ecuación \ 2\]
Sustituyendo la ecuación 2 en la ecuación 1, tenemos:
\[2x+\sqrt{2} x = 20\]
Factorizando
\[x\left(2+\sqrt{2}\right)=20\]
Despejando a $x$
\[x=\frac{20}{\left(2+\sqrt{2}\right)}\]
Racionalizando el denominador:
\[x=\frac{20\left(2-\sqrt{2}\right)}{\left(2+\sqrt{2}\right)\left(2-\sqrt{2}\right)}=\frac{40-20\sqrt{2}}{4-2}=\frac{40-20\sqrt{2}}{2}\]
\[x=20-10\sqrt{2}\]
Sustituyendo en la ecuación 2, obtenemos la medida de los lados del octágono:
\[y=\sqrt{2}\left(20-10\sqrt{2}\right)\]
\[y=20\sqrt{2}-20\]
Los lados del octágono miden $y=20\sqrt{2}-20$ cm
Actividad H5P
Instrucción para el alumno: ¡Es el momento de revisar lo aprendido!